题目内容
已知函数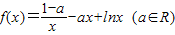
(1)当a=0时,求f(x)在
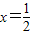 处切线的斜率;
处切线的斜率;(2)当
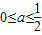 时,讨论f(x)的单调性;
时,讨论f(x)的单调性;(3)设g(x)=x2-2bx+3当
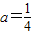 时,若对于任意x1∈(0,2),存在x2∈[1,2]使f(x1)≥g(x2)成立,求实数b的取值范围.
时,若对于任意x1∈(0,2),存在x2∈[1,2]使f(x1)≥g(x2)成立,求实数b的取值范围.
【答案】分析:(1)求导函数,令 ,即可求得切线的斜率;
,即可求得切线的斜率;
(2)分类讨论,利用导数的正负,即可得到函数的单调区间;
(3)原命题等价于g(x)在x∈[1,2]的最小值不大于f(x)在(0,2)上的最小值 ,由此可求实数b的取值范围.
,由此可求实数b的取值范围.
解答:解:(1)∵a=0,∴ ,
,
∴
则f(x)在 处切线的斜率
处切线的斜率 …(4分)
…(4分)
(2)函数f(x)的定义域为x∈(0,+∞),
①当a=0时, ,令f'(x)=0,解得x=1,
,令f'(x)=0,解得x=1,
∴x∈(0,1),f'(x)<0;x∈(1,+∞),f'(x)>0
∴函数f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1)…(6分)
②当 时,
时, ,解得x1=1或
,解得x1=1或 且x1<x2
且x1<x2
列表
由表可知函数f(x)的单调递减区间为(0,1);单调递增区间为 ,单调递减区间为
,单调递减区间为 ;
;
③当 时,
时, ,∴函数f(x)的单调递减区间为(0,+∞).…(10分)
,∴函数f(x)的单调递减区间为(0,+∞).…(10分)
(3) ,
, ,解得x1=1或x2=3
,解得x1=1或x2=3
∵x∈(0,2),∴f(x)的单调递减区间为(0,1);单调递增区间为(1,2),
∴f(x)的最小值为
原命题等价于g(x)在x∈[1,2]的最小值不大于f(x)在(0,2)上的最小值 ,
,
又g(x)=x2-2bx+3x∈[1,2]
①当b<1时,g(x)的最小值为g(1)=4-2b>2,不合;
②当b∈[1,2]时,g(x)的最小值为 ,解得
,解得 ;
;
③当b∈(2,+∞)时,g(x)的最小值为 ,解得b>2,
,解得b>2,
综上,b的取值范围 . …(14分)
. …(14分)
点评:本题考查导数知识的运用,考查切线的斜率,考查函数的单调性,考查函数的最值,考查分类讨论的数学思想,属于中档题.
 ,即可求得切线的斜率;
,即可求得切线的斜率;(2)分类讨论,利用导数的正负,即可得到函数的单调区间;
(3)原命题等价于g(x)在x∈[1,2]的最小值不大于f(x)在(0,2)上的最小值
 ,由此可求实数b的取值范围.
,由此可求实数b的取值范围.解答:解:(1)∵a=0,∴
 ,
,∴

则f(x)在
 处切线的斜率
处切线的斜率 …(4分)
…(4分)(2)函数f(x)的定义域为x∈(0,+∞),

①当a=0时,
 ,令f'(x)=0,解得x=1,
,令f'(x)=0,解得x=1,∴x∈(0,1),f'(x)<0;x∈(1,+∞),f'(x)>0
∴函数f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1)…(6分)
②当
 时,
时, ,解得x1=1或
,解得x1=1或 且x1<x2
且x1<x2列表
| x | (0,1) | 1 | (1, ) ) |  | ( ) ) |
| f′(x) | - | + | - | ||
| f(x) | ↓ | 极小值 | ↑ | 极大值 | ↓ |
 ,单调递减区间为
,单调递减区间为 ;
;③当
 时,
时, ,∴函数f(x)的单调递减区间为(0,+∞).…(10分)
,∴函数f(x)的单调递减区间为(0,+∞).…(10分)(3)
 ,
, ,解得x1=1或x2=3
,解得x1=1或x2=3∵x∈(0,2),∴f(x)的单调递减区间为(0,1);单调递增区间为(1,2),
∴f(x)的最小值为

原命题等价于g(x)在x∈[1,2]的最小值不大于f(x)在(0,2)上的最小值
 ,
,又g(x)=x2-2bx+3x∈[1,2]
①当b<1时,g(x)的最小值为g(1)=4-2b>2,不合;
②当b∈[1,2]时,g(x)的最小值为
 ,解得
,解得 ;
;③当b∈(2,+∞)时,g(x)的最小值为
 ,解得b>2,
,解得b>2,综上,b的取值范围
 . …(14分)
. …(14分)点评:本题考查导数知识的运用,考查切线的斜率,考查函数的单调性,考查函数的最值,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
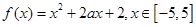
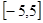 上是单调函数
上是单调函数 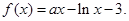
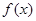 在点(1,-2)处的切线方程;
在点(1,-2)处的切线方程;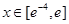 上的图象与直线
上的图象与直线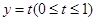 总有两个不同交点,求实数a的取值范围。
总有两个不同交点,求实数a的取值范围。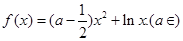
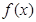 在区间[1,e]上的最大值和最小值;
在区间[1,e]上的最大值和最小值;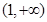 上,函数
上,函数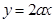 下方,求a的取值范围。
下方,求a的取值范围。
 的图象与直线y=ax只有一个公共点,求实数b的取值范围。
的图象与直线y=ax只有一个公共点,求实数b的取值范围。
 的图象与直线y=ax只有一个公共点,求实数b的取值范围。
的图象与直线y=ax只有一个公共点,求实数b的取值范围。