题目内容
 如图所示,抛物线形拱桥,当拱顶离水面3米,水面宽6米.如果水面上升1米,水面宽
如图所示,抛物线形拱桥,当拱顶离水面3米,水面宽6米.如果水面上升1米,水面宽2
| 6 |
2
米.| 6 |
分析:先建立平面直角坐标系,抛物线方程假设为:x2=-2py(p>0),再利用当拱顶离水面3米,水面宽6米,求出抛物线方程,进而可求水面上升1米,水面的宽.
解答: 解:建立如图所示的平面直角坐标系,则抛物线方程可假设为:x2=-2py(p>0)
解:建立如图所示的平面直角坐标系,则抛物线方程可假设为:x2=-2py(p>0)
∵当拱顶离水面3米,水面宽6米
∴A(3,-3)
代入抛物线方程可得:9=6p
∴2p=3
∴抛物线方程为:x2=-3y
如果水面上升1米,则令y=-2
∴x=±
∴水面宽为2
米
故答案为:2
 解:建立如图所示的平面直角坐标系,则抛物线方程可假设为:x2=-2py(p>0)
解:建立如图所示的平面直角坐标系,则抛物线方程可假设为:x2=-2py(p>0)∵当拱顶离水面3米,水面宽6米
∴A(3,-3)
代入抛物线方程可得:9=6p
∴2p=3
∴抛物线方程为:x2=-3y
如果水面上升1米,则令y=-2
∴x=±
| 6 |
∴水面宽为2
| 6 |
故答案为:2
| 6 |
点评:本题考查抛物线的应用,考查待定系数法求抛物线的方程,解题的关键是正确建立平面直角坐标系.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
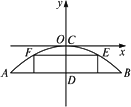
 ,当水位线在AB位置时,水面宽为12m,这时水面离桥顶的高度h是
,当水位线在AB位置时,水面宽为12m,这时水面离桥顶的高度h是
 m
m m
m ,当水位线在AB位置时,水面宽为12m,这时水面离桥顶的高度h是
,当水位线在AB位置时,水面宽为12m,这时水面离桥顶的高度h是
 m
m m
m