题目内容
定义:对于一个函数f(x)(x∈D),若存在两条距离为d的直线y=kx+m1和y=kx+m2,使得在x∈D时,kx+m1≤f(x)≤kx+m2恒成立,则称函数f(x)在D内有一个宽度为d的通道.下列函数:①f(x)=e-x,②f(x)=sinx,③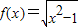 ,④f(x)=x2,其中在[1,+∞)有一个宽度为1的通道的函数的序号是 .
,④f(x)=x2,其中在[1,+∞)有一个宽度为1的通道的函数的序号是 .
【答案】分析:对于①,当x∈[1,+∞)时,确定函数的值域, ,故可知两条直线可取y=0,y=1;对于②,当x∈[1,+∞)时,-1≤sinx≤1;对于③,当x∈[1,+∞)时,
,故可知两条直线可取y=0,y=1;对于②,当x∈[1,+∞)时,-1≤sinx≤1;对于③,当x∈[1,+∞)时, ,表示双曲线x2-y2=1在第一象限的部分,双曲线的渐近线为y=x,故可取另一直线为
,表示双曲线x2-y2=1在第一象限的部分,双曲线的渐近线为y=x,故可取另一直线为 ,满足在[1,+∞)有一个宽度为1的通道;
,满足在[1,+∞)有一个宽度为1的通道;
对于④,当x∈[1,+∞)时,f(x)∈[1,+∞),故可得结论.
解答:解:对于①,当x∈[1,+∞)时, ,故在[1,+∞)有一个宽度为1的通道,两条直线可取y=0,y=1;
,故在[1,+∞)有一个宽度为1的通道,两条直线可取y=0,y=1;
对于②,当x∈[1,+∞)时,-1≤sinx≤1,故在[1,+∞)不存在一个宽度为1的通道;
对于③,当x∈[1,+∞)时, ,表示双曲线x2-y2=1在第一象限的部分,双曲线的渐近线为y=x,故可取另一直线为
,表示双曲线x2-y2=1在第一象限的部分,双曲线的渐近线为y=x,故可取另一直线为 ,满足在[1,+∞)有一个宽度为1的通道;
,满足在[1,+∞)有一个宽度为1的通道;
对于④,当x∈[1,+∞)时,f(x)∈[1,+∞),故在[1,+∞)不存在一个宽度为1的通道;
故答案为:①③
点评:本题考查的重点是对新定义的理解,解题的关键是通过研究函数的性质,找出满足题意的直线.
 ,故可知两条直线可取y=0,y=1;对于②,当x∈[1,+∞)时,-1≤sinx≤1;对于③,当x∈[1,+∞)时,
,故可知两条直线可取y=0,y=1;对于②,当x∈[1,+∞)时,-1≤sinx≤1;对于③,当x∈[1,+∞)时, ,表示双曲线x2-y2=1在第一象限的部分,双曲线的渐近线为y=x,故可取另一直线为
,表示双曲线x2-y2=1在第一象限的部分,双曲线的渐近线为y=x,故可取另一直线为 ,满足在[1,+∞)有一个宽度为1的通道;
,满足在[1,+∞)有一个宽度为1的通道;对于④,当x∈[1,+∞)时,f(x)∈[1,+∞),故可得结论.
解答:解:对于①,当x∈[1,+∞)时,
 ,故在[1,+∞)有一个宽度为1的通道,两条直线可取y=0,y=1;
,故在[1,+∞)有一个宽度为1的通道,两条直线可取y=0,y=1;对于②,当x∈[1,+∞)时,-1≤sinx≤1,故在[1,+∞)不存在一个宽度为1的通道;
对于③,当x∈[1,+∞)时,
 ,表示双曲线x2-y2=1在第一象限的部分,双曲线的渐近线为y=x,故可取另一直线为
,表示双曲线x2-y2=1在第一象限的部分,双曲线的渐近线为y=x,故可取另一直线为 ,满足在[1,+∞)有一个宽度为1的通道;
,满足在[1,+∞)有一个宽度为1的通道;对于④,当x∈[1,+∞)时,f(x)∈[1,+∞),故在[1,+∞)不存在一个宽度为1的通道;
故答案为:①③
点评:本题考查的重点是对新定义的理解,解题的关键是通过研究函数的性质,找出满足题意的直线.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
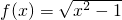 ,④f(x)=x2,其中在[1,+∞)有一个宽度为1的通道的函数的序号是________.
,④f(x)=x2,其中在[1,+∞)有一个宽度为1的通道的函数的序号是________.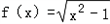 ,④f(x)=x2,
,④f(x)=x2,