题目内容
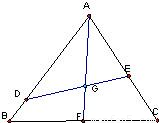
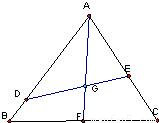
如图,已知点G是边长为1的正三角形ABC的中心,线段DE经过点G,并绕点G转动,分别交边AB、AC于点D、E;设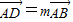 ,
,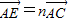 ,其中0<m≤1,0<n≤1.
,其中0<m≤1,0<n≤1.(1)求表达式
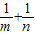 的值,并说明理由;
的值,并说明理由;(2)求△ADE面积的最大和最小值,并指出相应的m、n的值.
【答案】分析:(1)将向量 用向量
用向量 表达,由D、G、E三点共线,即可得到m和n的关系.
表达,由D、G、E三点共线,即可得到m和n的关系.
(2)由三角形面积公式,SΛADE= mn,由(1)可知
mn,由(1)可知 =3,由消元法n=
=3,由消元法n= ,转化为m的函数求最值即可.
,转化为m的函数求最值即可.
解答:解:(1)如图延长AG交BC与F,∵G为△ABC的中心
∴F为BC的中点,则有
∵ ,
, ,
,
∴ 即
即
∵D、G、E三点共线
∴
故 =3
=3
 (2)∵△ABC是边长为1的正三角形,
(2)∵△ABC是边长为1的正三角形,
∴|AD|=m,|AE|=n∴SΛADE= mn
mn
由 =3,0<m≤1,0<n≤1
=3,0<m≤1,0<n≤1
∴n= ,
, 即
即 .
.
∴SΛADE= mn=
mn=

设t=m- 则m=t+
则m=t+ (
( )
)
∴SΛADE= mn=
mn= (t+
(t+ +
+ )
)
易知 在
在 为减函数,在
为减函数,在 为增函数.
为增函数.
∴t= ,即
,即 ,时,f(t)取得最小值
,时,f(t)取得最小值 ,
,
即SΛADE取得最小值
又 ,
,
∴f(t)取得最大值是 ,
,
则SΛADE取得最大值 ,此时
,此时 或
或
点评:本题考查平面向量基本定理和向量的表示、求函数的最值,考查消元和换元等方法.
 用向量
用向量 表达,由D、G、E三点共线,即可得到m和n的关系.
表达,由D、G、E三点共线,即可得到m和n的关系.(2)由三角形面积公式,SΛADE=
 mn,由(1)可知
mn,由(1)可知 =3,由消元法n=
=3,由消元法n= ,转化为m的函数求最值即可.
,转化为m的函数求最值即可.解答:解:(1)如图延长AG交BC与F,∵G为△ABC的中心
∴F为BC的中点,则有

∵
 ,
, ,
,
∴
 即
即
∵D、G、E三点共线
∴

故
 =3
=3 (2)∵△ABC是边长为1的正三角形,
(2)∵△ABC是边长为1的正三角形,∴|AD|=m,|AE|=n∴SΛADE=
 mn
mn由
 =3,0<m≤1,0<n≤1
=3,0<m≤1,0<n≤1∴n=
 ,
, 即
即 .
.∴SΛADE=
 mn=
mn=

设t=m-
 则m=t+
则m=t+ (
( )
)∴SΛADE=
 mn=
mn= (t+
(t+ +
+ )
)易知
 在
在 为减函数,在
为减函数,在 为增函数.
为增函数.∴t=
 ,即
,即 ,时,f(t)取得最小值
,时,f(t)取得最小值 ,
,即SΛADE取得最小值

又
 ,
,∴f(t)取得最大值是
 ,
,则SΛADE取得最大值
 ,此时
,此时 或
或
点评:本题考查平面向量基本定理和向量的表示、求函数的最值,考查消元和换元等方法.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
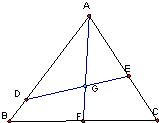 如图,已知点G是边长为1的正三角形ABC的中心,线段DE经过点G,并绕点G转动,分别交边AB、AC于点D、E;设
如图,已知点G是边长为1的正三角形ABC的中心,线段DE经过点G,并绕点G转动,分别交边AB、AC于点D、E;设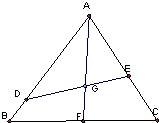 如图,已知点G是边长为1的正三角形ABC的中心,线段DE经过点G,并绕点G转动,分别交边AB、AC于点D、E;设
如图,已知点G是边长为1的正三角形ABC的中心,线段DE经过点G,并绕点G转动,分别交边AB、AC于点D、E;设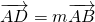 ,
,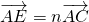 ,其中0<m≤1,0<n≤1.
,其中0<m≤1,0<n≤1. 的值,并说明理由;
的值,并说明理由;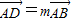 ,
,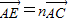 ,其中0<m≤1,0<n≤1.
,其中0<m≤1,0<n≤1.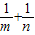 的值,并说明理由;
的值,并说明理由;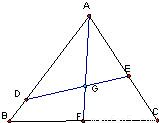
 ,
,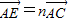 ,其中0<m≤1,0<n≤1.
,其中0<m≤1,0<n≤1.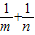 的值,并说明理由;
的值,并说明理由;