题目内容
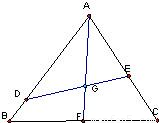
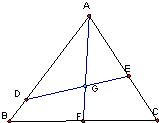 如图,已知点G是边长为1的正三角形ABC的中心,线段DE经过点G,并绕点G转动,分别交边AB、AC于点D、E;设
如图,已知点G是边长为1的正三角形ABC的中心,线段DE经过点G,并绕点G转动,分别交边AB、AC于点D、E;设| AD |
| AB |
| AE |
| AC |
(1)求表达式
| 1 |
| m |
| 1 |
| n |
(2)求△ADE面积的最大和最小值,并指出相应的m、n的值.
分析:(1)将向量
用向量
表达,由D、G、E三点共线,即可得到m和n的关系.
(2)由三角形面积公式,SΛADE=
mn,由(1)可知
+
=3,由消元法n=
,转化为m的函数求最值即可.
| AG |
| AD |
| 和AE |
(2)由三角形面积公式,SΛADE=
| ||
| 4 |
| 1 |
| m |
| 1 |
| n |
| m |
| 3m-1 |
解答:解:(1)如图延长AG交BC与F,∵G为△ABC的中心
∴F为BC的中点,则有
=
+
∵
=m
,
=n
,
=
∴
=
+
即
=
+
∵D、G、E三点共线
∴
+
=1
故
+
=3
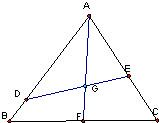 (2)∵△ABC是边长为1的正三角形,
(2)∵△ABC是边长为1的正三角形,
∴|AD|=m,|AE|=n∴SΛADE=
mn
由
+
=3,0<m≤1,0<n≤1
∴n=
,1≤
≤2即
≤m≤1.
∴SΛADE=
mn=
设t=m-
则m=t+
(
≤t≤
)
∴SΛADE=
mn=
(t+
+
)
易知f(t)=t+
在[
,
]为减函数,在[
,
]为增函数.
∴t=
,即m=n=
,时,f(t)取得最小值
,
即SΛADE取得最小值
又f(
)=f(
)=
,
∴f(t)取得最大值是
,
则SΛADE取得最大值
,此时m=
,n=
或m=1,n=
∴F为BC的中点,则有
| AF |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AC |
∵
| AD |
| AB |
| AE |
| AC |
| AG |
| 2 |
| 3 |
| AF |
∴
| 3 |
| 2 |
| AG |
| 1 |
| 2m |
| AD |
| 1 |
| 2n |
| AE |
| AG |
| 1 |
| 3m |
| AD |
| 1 |
| 3n |
| AE |
∵D、G、E三点共线
∴
| 1 |
| 3m |
| 1 |
| 3n |
故
| 1 |
| m |
| 1 |
| n |
 (2)∵△ABC是边长为1的正三角形,
(2)∵△ABC是边长为1的正三角形,∴|AD|=m,|AE|=n∴SΛADE=
| ||
| 4 |
由
| 1 |
| m |
| 1 |
| n |
∴n=
| m |
| 3m-1 |
| 1 |
| m |
| 1 |
| 2 |
∴SΛADE=
| ||
| 4 |
| ||
| 4 |
| m2 |
| 3m-1 |
设t=m-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 6 |
| 2 |
| 3 |
∴SΛADE=
| ||
| 4 |
| ||
| 12 |
| 1 |
| 9t |
| 2 |
| 3 |
易知f(t)=t+
| 1 |
| 9t |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
∴t=
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
即SΛADE取得最小值
| ||
| 9 |
又f(
| 1 |
| 6 |
| 2 |
| 3 |
| 5 |
| 6 |
∴f(t)取得最大值是
| 5 |
| 6 |
则SΛADE取得最大值
| ||
| 8 |
| 1 |
| 2 |
| 2 |
| 5 |
| 1 |
| 2 |
点评:本题考查平面向量基本定理和向量的表示、求函数的最值,考查消元和换元等方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
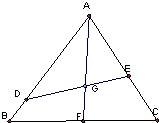 如图,已知点G是边长为1的正三角形ABC的中心,线段DE经过点G,并绕点G转动,分别交边AB、AC于点D、E;设
如图,已知点G是边长为1的正三角形ABC的中心,线段DE经过点G,并绕点G转动,分别交边AB、AC于点D、E;设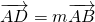 ,
,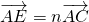 ,其中0<m≤1,0<n≤1.
,其中0<m≤1,0<n≤1. 的值,并说明理由;
的值,并说明理由;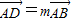 ,
,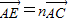 ,其中0<m≤1,0<n≤1.
,其中0<m≤1,0<n≤1.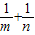 的值,并说明理由;
的值,并说明理由;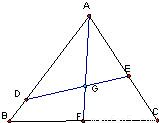
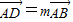 ,
,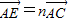 ,其中0<m≤1,0<n≤1.
,其中0<m≤1,0<n≤1.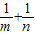 的值,并说明理由;
的值,并说明理由;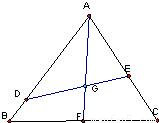
 ,
,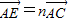 ,其中0<m≤1,0<n≤1.
,其中0<m≤1,0<n≤1.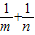 的值,并说明理由;
的值,并说明理由;