题目内容
设函数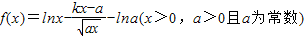 .
.(1)当k=1时,判断函数f(x)的单调性,并加以证明;
(2)当k=0时,求证:f(x)>0对一切x>0恒成立;
(3)若k<0,且k为常数,求证:f(x)的极小值是一个与a无关的常数.
【答案】分析:(1)求出函数的导函数,判断出导函数小于等于0,判断出函数单调性.
(2)求出导函数,令导函数为0,求出根,判断出根左右两边的符号,求出极小值,判断出极小值的符号得证.
(3)求出导函数,令导函数为0,求出根,判断根左右两边的符号,求出极小值,判断出极小值是与a无关的常数.
解答:解:(1)函数的定义域为x>0
当k=1时,f(x)=
∵ =
=
∴函数f(x)在(0,+∞)上是单调减函数
(2)当k=0时,

令
当

∴
∵e>2
∴
∴f(x)>0恒成立
(3)∵
∴
令
解得 (
( 舍去)
舍去)
∴
 ,f′(x)<0,f(x)是单调减函数
,f′(x)<0,f(x)是单调减函数
 时,f′(x)>0,f(x)是单调增函数
时,f′(x)>0,f(x)是单调增函数
因此,当x= f(x)有极小值
f(x)有极小值
令
∵ 而
而 是与a无关的常数
是与a无关的常数
∴ 均与a无关.
均与a无关.
∴f(x)是与a无关的常数.
则f(x)的极小值是一个与a无关的常数.
点评:求函数的极小值时,令导函数为0求出根,但一定注意判断根左右两边的符号是否异号.
(2)求出导函数,令导函数为0,求出根,判断出根左右两边的符号,求出极小值,判断出极小值的符号得证.
(3)求出导函数,令导函数为0,求出根,判断根左右两边的符号,求出极小值,判断出极小值是与a无关的常数.
解答:解:(1)函数的定义域为x>0
当k=1时,f(x)=

∵
 =
=
∴函数f(x)在(0,+∞)上是单调减函数
(2)当k=0时,


令

当


∴

∵e>2
∴

∴f(x)>0恒成立
(3)∵

∴

令

解得
 (
( 舍去)
舍去)∴

 ,f′(x)<0,f(x)是单调减函数
,f′(x)<0,f(x)是单调减函数 时,f′(x)>0,f(x)是单调增函数
时,f′(x)>0,f(x)是单调增函数因此,当x=
 f(x)有极小值
f(x)有极小值令

∵
 而
而 是与a无关的常数
是与a无关的常数∴
 均与a无关.
均与a无关.∴f(x)是与a无关的常数.
则f(x)的极小值是一个与a无关的常数.
点评:求函数的极小值时,令导函数为0求出根,但一定注意判断根左右两边的符号是否异号.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
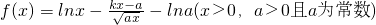 .
.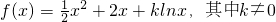 .
. .
.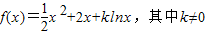 .
.