题目内容
中心在坐标原点,焦点在y轴上的椭圆,其一个焦点与短轴两端点的加线互相垂直,且此焦点与椭圆上的点之间的距离最小值为 ,则椭圆的标准方程为________.
,则椭圆的标准方程为________.

分析:可设所求椭圆的标准方程为
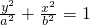 (a>b>0),由题意可得a-c=
(a>b>0),由题意可得a-c= ,a=
,a= c,从而可求其方程.
c,从而可求其方程.解答:设椭圆的标准方程为
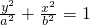 (a>b>0),
(a>b>0),∵该椭圆的一个焦点与椭圆上的点之间的距离最小值为
 ,
,∴a-c=
 ①,
①,又一个焦点与短轴两端点的加线互相垂直,
∴a=
 c②,
c②,由①②可得a=
 ,c=
,c= ,
,∴b2=a2-c2=5,
∴所求椭圆的标准方程为:
 .
.故答案为:
 .
.点评:本题考查椭圆的简单性质与椭圆的标准方程,关键在于理解题意,得到关于a、c的关系式,着重考查待定系数法求椭圆的标准方程,属于中档题.

练习册系列答案
相关题目
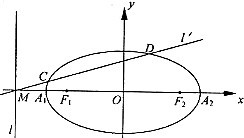 已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,
已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M, (2011•延庆县一模)已知椭圆C的中心在坐标原点,焦点在x轴上,它的一个顶点B与抛物线x2=4y的焦点重合,离心率
(2011•延庆县一模)已知椭圆C的中心在坐标原点,焦点在x轴上,它的一个顶点B与抛物线x2=4y的焦点重合,离心率