题目内容
函数
的单调递减区间为________．
（3，+∞）
分析：利用复合函数的单调性，只需求g（x）=x2-2x-3在g（x）＞0的情况下的递增区间即可．
解答：令g（x）=x2-2x-3，则f（x）=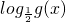
为复合函数，
由题意得，函数 的单调递减区间为g（x）=x2-2x-3在g（x）＞0的情况下的递增区间，
∴由x2-2x-3＞0得：x＞3或x＜-1，
又g（x）=x2-2x-3的递增区间为：[1，+∞），
∴x＞3，即函数 的单调递减区间为（3，+∞）．
故答案为：（3，+∞）．
点评：本题考查复合函数的单调性，着重考查对数函数的单调性，突出分析问题，解决问题能力的考查，属于中档题．
分析：利用复合函数的单调性，只需求g（x）=x2-2x-3在g（x）＞0的情况下的递增区间即可．
解答：令g（x）=x2-2x-3，则f（x）=
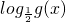为复合函数，由题意得，函数
的单调递减区间为g（x）=x2-2x-3在g（x）＞0的情况下的递增区间，∴由x2-2x-3＞0得：x＞3或x＜-1，
又g（x）=x2-2x-3的递增区间为：[1，+∞），
∴x＞3，即函数
的单调递减区间为（3，+∞）．故答案为：（3，+∞）．
点评：本题考查复合函数的单调性，着重考查对数函数的单调性，突出分析问题，解决问题能力的考查，属于中档题．
练习册系列答案
相关题目