题目内容
设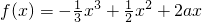
(1)若f(x)在 上存在单调递增区间,求a的取值范围.
上存在单调递增区间,求a的取值范围.
(2)当0<a<2时,f(x)在[1,4]的最小值为 ,求f(x)在该区间上的最大值.
,求f(x)在该区间上的最大值.
解:(1)f′(x)=-x2+x+2a
f(x)在 存在单调递增区间
存在单调递增区间
∴f′(x)>0在 有解
有解
∵f′(x)=-x2+x+2a对称轴为
∴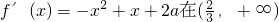 递减
递减
∴
解得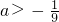 .
.
(2)当0<a<2时,△>0;
f′(x)=0得到两个根为 ;
; (舍)
(舍)
∵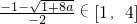
∴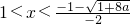 时,f′(x)>0;
时,f′(x)>0; 时,f′(x)<0
时,f′(x)<0
当x=1时,f(1)=2a+ ;当x=4时,f(4)=8a
;当x=4时,f(4)=8a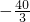 <f(1)
<f(1)
当x=4时最小∴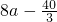 =
= 解得a=1
解得a=1
所以当x=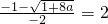 时最大为
时最大为
分析:(1)利用函数递增,导函数大于0恒成立,求出导函数的最大值,使最大值大于0.
(2)求出导函数的根,判断出根左右两边的导函数的符号,求出端点值的大小,求出最小值,列出方程求出a,求出最大值.
点评:本题考查利用导函数求参数的范围、利用导函数求函数的单调性、求函数的最值.
f(x)在
 存在单调递增区间
存在单调递增区间∴f′(x)>0在
 有解
有解∵f′(x)=-x2+x+2a对称轴为

∴
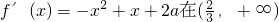 递减
递减∴

解得
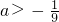 .
.(2)当0<a<2时,△>0;
f′(x)=0得到两个根为
 ;
; (舍)
(舍)∵
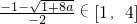
∴
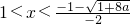 时,f′(x)>0;
时,f′(x)>0; 时,f′(x)<0
时,f′(x)<0当x=1时,f(1)=2a+
 ;当x=4时,f(4)=8a
;当x=4时,f(4)=8a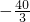 <f(1)
<f(1)当x=4时最小∴
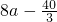 =
= 解得a=1
解得a=1所以当x=
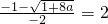 时最大为
时最大为
分析:(1)利用函数递增,导函数大于0恒成立,求出导函数的最大值,使最大值大于0.
(2)求出导函数的根,判断出根左右两边的导函数的符号,求出端点值的大小,求出最小值,列出方程求出a,求出最大值.
点评:本题考查利用导函数求参数的范围、利用导函数求函数的单调性、求函数的最值.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
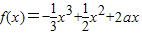
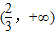 上存在单调递增区间,求a的取值范围.
上存在单调递增区间,求a的取值范围.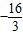 ,求f(x)在该区间上的最大值.
,求f(x)在该区间上的最大值.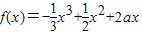
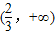 上存在单调递增区间,求a的取值范围.
上存在单调递增区间,求a的取值范围.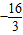 ,求f(x)在该区间上的最大值.
,求f(x)在该区间上的最大值.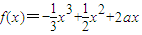
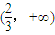 上存在单调递增区间,求a的取值范围.
上存在单调递增区间,求a的取值范围.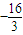 ,求f(x)在该区间上的最大值.
,求f(x)在该区间上的最大值.