题目内容
三角形 中,设
中,设 ,若
,若 ,则三角形
,则三角形 的形状是( )
的形状是( )
| A.锐角三角形 | B.钝角三角形 | C.直角三角形 | D.无法确定 |
B
解析试题分析:如图 ,由
,由 即可得
即可得 与
与 的夹角为钝角,由于
的夹角为钝角,由于 .所以
.所以 为钝角.所以选B.
为钝角.所以选B.
考点:1.向量的和差运算.2.向量的数量积.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
等腰直角三角形 中,
中, 是斜边
是斜边 的中点,若
的中点,若 ,则
,则 =( )
=( )
A. | B. | C. | D. |
若A ,B
,B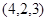 ,C
,C ,则△ABC的形状是( )
,则△ABC的形状是( )
| A.锐角三角形 | B.直角三角形 |
| C.钝角三角形 | D.等腰三角形 |
已知向量a=(sin θ, ),b=(1,
),b=(1, ),其中θ∈
),其中θ∈ ,则一定有 ( )
,则一定有 ( )
| A.a∥b | B.a⊥b | C.a与b的夹角为45° | D.|a|=|b| |
平面向量 满足
满足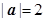 ,
,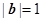 ,且
,且 的夹角为
的夹角为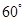 ,则
,则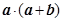 = ( )
= ( )
| A.1 | B.3 | C.5 | D.7 |
在△ABC中, ,则角A的最大值为( )
,则角A的最大值为( )
A. | B. | C. | D. |
设向量 =(1,
=(1, )与
)与 =(-1,2
=(-1,2 )垂直,则
)垂直,则 等于 ( )
等于 ( )
A. | B. |
| C.0 | D.-1 |
已知△ABC中, =a,
=a, =b,a·b<0,
=b,a·b<0, ,|a|=3,|b|=5,
,|a|=3,|b|=5,
则a与b的夹角是( )
| A.30° |
| B.150° |
| C.210° |
| D.30°或150° |
点P是底边长为2 ,高为2的正三棱柱表面上的动点,MN是该棱柱内切球的一条直径,则
,高为2的正三棱柱表面上的动点,MN是该棱柱内切球的一条直径,则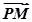 ·
·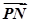 的取值范围是( )
的取值范围是( )
| A.[0,2] | B.[0,3] |
| C.[0,4] | D.[-2,2] |