Question

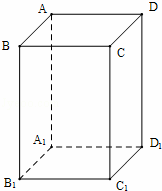
已知ABCD﹣A₁B₁C₁D₁是底面边长为1的正四棱柱，高AA₁=2，求：

（1）异面直线BD与AB₁所成的角的大小的余弦值

（2）四面体AB₁D₁C的体积．

Answer 1

解答：

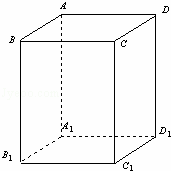
解：（1）连接DC₁，BC₁，

易知DC₁∥AB₁，

∴∠BDC₁就是异面直线BD 与AB₁ 所成角，

在△BDC₁中，DC₁=BC₁=，BD=，

∴cos∠BDC₁==．

所以异面直线BD与AB₁所成的角的大小的余弦值为．

（2）=﹣﹣﹣﹣

而V_{ABCD﹣AB1C1D1}=S_ABCD•AA₁=1×2=2，

V_B1﹣ABC=V_D1﹣ACD=V_DA1C1D1=V_B﹣A1B1C1=××2．

∴V_A﹣B1D1C═2﹣4×××2=．

所以四面体AB₁D₁C的体积为．

点评：

此题是个基础题．考查异面直线所成角和棱锥的体积问题，求解方法一般是平移法，转化为平面角问题来解决，和利用割补法求棱锥的体积问题，体现了数形结合和转化的思想．