题目内容
若锐角α，β满足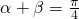
，则（1+tanα）•（1+tanβ）=________．
2
分析：由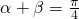，两边求正切，左边利用两角和与差的正切函数公式化简，右边利用特殊角的三角函数值化简，得到关于tanα和tanβ的关系式，表示出tanα+tanβ，把所求式子去括号化简后，将表示出的tanα+tanβ代入，化简可求出值．
解答：∵，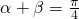
∴tan（α+β）=
=1，
即tanα+tanβ=1-tanαtanβ，
则（1+tanα）•（1+tanβ）
=1+tanα+tanβ+tanαtanβ
=1+1-tanαtanβ+tanαtanβ
=2．
故答案为：2
点评：此题考查了两角和与差的正切函数公式，以及特殊角的三角函数值，利用了整体代入的思想，熟练掌握公式是解本题的关键．
分析：由
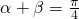，两边求正切，左边利用两角和与差的正切函数公式化简，右边利用特殊角的三角函数值化简，得到关于tanα和tanβ的关系式，表示出tanα+tanβ，把所求式子去括号化简后，将表示出的tanα+tanβ代入，化简可求出值．解答：∵
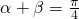，∴tan（α+β）=
=1，即tanα+tanβ=1-tanαtanβ，
则（1+tanα）•（1+tanβ）
=1+tanα+tanβ+tanαtanβ
=1+1-tanαtanβ+tanαtanβ
=2．
故答案为：2
点评：此题考查了两角和与差的正切函数公式，以及特殊角的三角函数值，利用了整体代入的思想，熟练掌握公式是解本题的关键．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
，
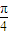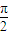），则f（sinθ）＞f（cosθ）；
；
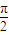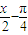）的图象，只需将y=sin
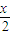的图象向左平移
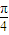个单位．
，则cosα的值为（ ）
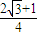
平移可得曲线（x+1）2-（y-3）2=1；
，则动点P的轨迹为双曲线；
与
夹角为锐角θ，且满足 
，则点P的轨迹是圆（除去与直线AB的交点）；
，则cosα的值为（ ）
，则cosα的值为（ ）
