题目内容
(本题14![]() 分)如图,五面体
分)如图,五面体![]()
![]() 中
中![]()
![]() ,
,![]() .底面
.底面![]() 是正三角形,
是正三角形,![]() .
.![]() 四边形
四边形![]() 是矩形
是矩形![]() ,
,![]() 二面角
二面角![]()
![]() 为直二面角.
为直二面角.
(1)![]() 在
在![]()
![]() 上运动,当
上运动,当![]() 在何处时,有
在何处时,有![]() ∥平面
∥平面![]() ,并且
,并且![]() 说明理由;
说明理由;
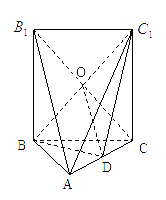
![]()
![]() (2)当
(2)当![]() ∥平面
∥平面![]() 时,求二面角
时,求二面角![]()
![]() 的
的![]() 余弦值.
余弦值.
(Ⅰ)略 (Ⅱ) ![]()
解析:
(Ⅰ)当![]() 为
为![]() 中点时,有
中点时,有![]() ∥平面
∥平面![]() .…1分
.…1分
证明:连结![]() 连结
连结![]() ,
,
∵四边形![]() 是矩形 ∴
是矩形 ∴![]() 为
为![]() 中点
中点![]()
 ∵
∵![]() ∥平面
∥平面![]() ,且
,且![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ∴
∴![]() ∥
∥![]() , ----
, ----![]() 5分
5分
∴![]() 为
为![]() 的中点. --6分
的中点. --6分![]()
![]()
(Ⅱ)建立空间直角坐标系![]() 如
如![]() 图所示,
图所示,
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ------------8分
------------8分
所以![]()
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则有 ,
,
即
令![]() ,
,![]() 可得
可得![]() 平面
平面![]() 的一个
的一个
法向量为![]() , ----------------11分
, ----------------11分
而平面![]() 的法向量为
的法向量为![]() , ---------------------------12
, ---------------------------12![]() 分
分
所以![]()

![]() ,
,
所以二面角![]()
![]() 的
的![]() 余弦值
余弦值![]() 为
为![]() --------14分
--------14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图,
如图,

 中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点
中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点