题目内容
设函数g（x）=x2-2，f（x）=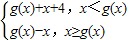
，则f（x）的值域是（ ）A．
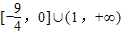
B．[0，+∞）
C．
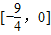
D．
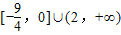
【答案】分析：根据x的取值范围化简f（x）的解析式，将解析式化到完全平方与常数的代数和形式，在每一段上求出值域，再把值域取并集．
解答：解：x＜g（x），即 x＜x2-2，即 x＜-1 或 x＞2． x≥g（x），即-1≤x≤2．
由题意 f（x）=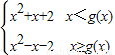
=
=
，
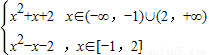
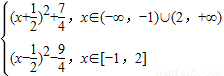所以当x∈（-∞，-1）∪（2，+∞）时，由二次函数的性质可得 f（x）∈（2，+∞）；
x∈[-1，2]时，由二次函数的性质可得f（x）∈[-
，0]，
故选 D．
点评：本题考查分段函数值域的求法，二次函数的性质的应用，考查分类讨论的数学思想，属于基础题．
解答：解：x＜g（x），即 x＜x2-2，即 x＜-1 或 x＞2． x≥g（x），即-1≤x≤2．
由题意 f（x）=
==
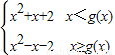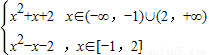
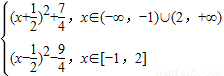，所以当x∈（-∞，-1）∪（2，+∞）时，由二次函数的性质可得 f（x）∈（2，+∞）；
x∈[-1，2]时，由二次函数的性质可得f（x）∈[-
，0]，故选 D．
点评：本题考查分段函数值域的求法，二次函数的性质的应用，考查分类讨论的数学思想，属于基础题．
练习册系列答案
相关题目