题目内容

点P在椭圆 $数学公式$ 上，椭圆的左准线为直线l，左焦点为F，作PQ⊥l于点Q，若P、F、Q三点构成一个等腰直角三角形，则该椭圆的离心率为________．

$\text{[math]}$
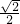
分析：根据椭圆的左准线为直线l，左焦点为F，作PQ⊥l于点Q，可得 $\text{[math]}$ ，利用P、F、Q三点构成一个等腰直角三角形，即可求得椭圆的离心率．
解答：∵椭圆的左准线为直线l，左焦点为F，作PQ⊥l于点Q
∴ $\text{[math]}$
∵P、F、Q三点构成一个等腰直角三角形
∴ $\text{[math]}$
∴ $\text{[math]}$
故答案为： $\text{[math]}$
点评：本题考查椭圆的第二定义与性质，考查等腰直角三角形的性质，属于基础题．

练习册系列答案

大联考单元期末测试卷系列答案

大赢家考前巧复习系列答案

大中考系列答案

单元测评导评导测导考系列答案

单元测试卷湖南教育出版社系列答案

单元达标卷系列答案

单元过关目标检测卷系列答案

天舟文化单元练测卷系列答案

单元巧练章节复习手册系列答案

学习指导与评价系列答案

相关题目

（1）如图1，已知定点F₁（-2，0）、F₂（2，0），动点N满足|

|=1（O为坐标原点），

（λ∈R），

=0，求点P的轨迹方程．

（2）如图2，已知椭圆C：

+y²=1的上、下顶点分别为A、B，点P在椭圆上，且异于点A、B，直线AP、BP与直线l：y=-2分别交于点M、N，
（ⅰ）设直线AP、BP的斜率分别为k₁、k₂，求证：k₁•k₂为定值；
（ⅱ）当点P运动时，以MN为直径的圆是否经过定点？请证明你的结论．

设椭圆中心在原点，两焦点F₁，F₂在x轴上，点P在椭圆上.若椭圆的离心率为，△PF₁F₂的周长为12，则椭圆的标准方程是

A.＋＝1 B.＋＝1 C.＋＝1 D.＋＝1

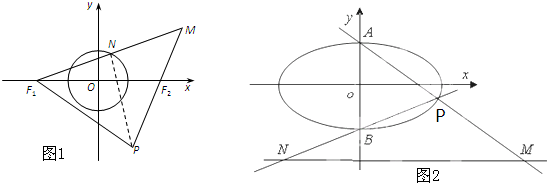
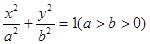点P在椭圆上，椭圆的左准线为直线l，左焦点为F，作PQ⊥l于点Q，若P、F、Q三点构成一个等腰直角三角形，则该椭圆的离心率为

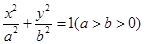如图，点P在椭圆上，F₁、F₂分别

是椭圆的左、右焦点，过点P作椭圆右准线的垂线，垂足为M，

若四边形为菱形，则椭圆的离心率是

如图，点P在椭圆上，F₁、F₂分别是椭圆的左、右焦点，过点P作椭圆右准线的垂线，垂足为M，若四边形为菱形，则椭圆的离心率是 .