题目内容
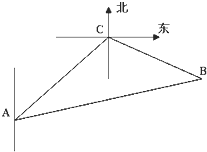一缉私艇（在A处）发现，在其北偏东45°方向相距24海里的海面上（C处）有一艘走私船遇正以12海里/小时的速度沿南偏东75°方向逃窜，若缉私船的速度为12| 3 |
分析：缉私艇与走私船原来的位置分别为A、C，在B处两船相遇，由条件得到∠ACB=120°，AC=24海里，设缉私船t小时后追上该走私船，根据各自的速度表示出BC与AB，由∠ACB=120°，∠CAB=α，利用正弦定理列出关系式，求出sinα的值；由余弦定理列出关于t的方程，求出方程的解即可得到t的值．
解答：解：由条件知∠ACB=120°，AC=24海里，
设缉私船t小时后追上该走私船，可得BC=12t，AB=12
t，
∴由正弦定理
=
得：
=
，
∴sinα=
，α=30°
由余弦定理AB2=AC2+BC2-2AC•BCcos∠ACB得：（12
t）2=242+（12t）2-2×24×12tcos120°，
解得：t=2，
∴t=2小时，α=30°．
追及所需的时间为2小时，α角的大小为30°．
设缉私船t小时后追上该走私船，可得BC=12t，AB=12
| 3 |
∴由正弦定理
| BC |
| sin∠CAB |
| AB |
| sin∠ACB |
| 12t |
| sinα |
12
| ||
| sin120° |
∴sinα=
| 1 |
| 2 |
由余弦定理AB2=AC2+BC2-2AC•BCcos∠ACB得：（12
| 3 |
解得：t=2，
∴t=2小时，α=30°．
追及所需的时间为2小时，α角的大小为30°．
点评：此题考查了正弦、余弦定理，以及特殊角的三角函数值，熟练掌握正弦、余弦定理是解本题的关键．
练习册系列答案
相关题目
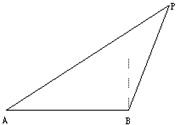一艘海岸缉私艇巡逻至A处时发现在其正东方向20km的海面B处有一艘走私船正以vkm/h的速度向北偏东30°的方向逃窜，缉私艇以
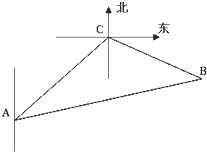一缉私艇（在A处）发现，在其北偏东45°方向相距24海里的海面上（C处）有一艘走私船遇正以12海里/小时的速度沿南偏东75°方向逃窜，若缉私船的速度为
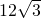海里/小时．若要在最短的时间内追上该走私船，缉私船应沿北偏东45°+α的方向去追，求追及所需的时间和α角的大小．
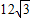海里/小时．若要在最短的时间内追上该走私船，缉私船应沿北偏东45°+α的方向去追，求追及所需的时间和α角的大小．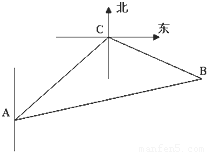
vkm/h的速度沿 的方向追击，能最快截获走私船？若v=40
，则追击时间至少为 分钟．