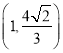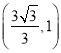题目内容
【题目】对于函数![]() ,若存在定义域
,若存在定义域![]() 内某个区间
内某个区间![]() ,使得
,使得![]() 在
在![]() 上的值域也是
上的值域也是![]() ,则称函数
,则称函数![]() 在定义域
在定义域![]() 上封闭.如果函数
上封闭.如果函数![]() 在
在![]() 上封闭,那么实数
上封闭,那么实数![]() 的取值范围是______.
的取值范围是______.
【答案】![]()
【解析】
先用定义证明函数![]() 在
在![]() 上递增,再根据奇偶性可得函数
上递增,再根据奇偶性可得函数![]() 在
在![]() 上为增函数,然后讨论
上为增函数,然后讨论![]() 和
和![]() 可得
可得![]() 的单调性,当
的单调性,当![]() 时,依题意可得
时,依题意可得![]() 是
是![]() 的两个不同的实数解,由此可解得
的两个不同的实数解,由此可解得![]() .当
.当![]() 时,依题意可得
时,依题意可得![]() ,由此可推出
,由此可推出![]() .
.
.设![]() ,则
,则![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以函数![]() 在
在![]() 上递增,
上递增,
又函数![]() 为奇函数,所以函数
为奇函数,所以函数![]() 在
在![]() 上为增函数,
上为增函数,
当![]() 时,函数
时,函数![]() 为增函数, 因为
为增函数, 因为![]() 在
在![]() 上的值域也是
上的值域也是![]() ,所以
,所以![]() ,即
,即 ,
,
即![]() 是
是![]() 的两个不同的实数解,解得
的两个不同的实数解,解得![]() 或
或![]() ,
,
由![]() 得
得![]() ,
,
当![]() 时,
时,![]() 为递减函数, 因为
为递减函数, 因为![]() 在
在![]() 上的值域也是
上的值域也是![]() ,所以
,所以![]() ,即
,即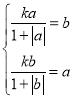 ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,因为
,因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() ,所以
,所以![]() ,即
,即![]() .
.
综上所述:![]() 或
或![]() .
.
故答案为: ![]() .
.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目