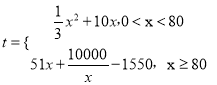题目内容
【题目】某班![]() 名学生在一次坐位体前屈测试中,成绩全部介于
名学生在一次坐位体前屈测试中,成绩全部介于![]() 与
与![]() 之间,将测试结果按如下方式分成五组:第一组
之间,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,…,第五组
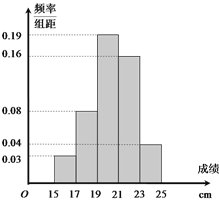
,…,第五组![]() ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.
(Ⅰ)若成绩大于或等于![]() 且小于
且小于![]() 认为良好,求该班在这次坐位体前屈测试中成绩良好的人数;
认为良好,求该班在这次坐位体前屈测试中成绩良好的人数;
(Ⅱ)若成绩之差的绝对值大于![]() 认为两位学生的身体韧度存在明显差异.现从第一、五组中随机取出两个成绩,求这两位学生的身体韧度存在明显差异的概率.
认为两位学生的身体韧度存在明显差异.现从第一、五组中随机取出两个成绩,求这两位学生的身体韧度存在明显差异的概率.
【答案】(Ⅰ) ![]() 人;(Ⅱ)
人;(Ⅱ) ![]()
【解析】试题分析:
(Ⅰ)利用频率分布直方图对应的概率值结合总人数可得该班成绩良好的人数为![]() 人.
人.
(Ⅱ)利用题意列出所有可能的事件,结合古典概型公式可得: ![]() .
.
试题解析:
(Ⅰ)由频率分布直方图知,
成绩在![]() 内的人数为:
内的人数为: ![]() (人),
(人),
所以该班成绩良好的人数为![]() 人.
人.
(Ⅱ)由频率分布直方图知:成绩在![]() 的人数为
的人数为![]() 人,设为
人,设为![]() ,
, ![]() ,
, ![]() ;成绩在
;成绩在![]() 的人数为
的人数为![]() 人,设为
人,设为![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
若![]() ,
, ![]() 时,有
时,有![]() ,
, ![]() ,
, ![]()
![]() 种情况;
种情况;
若![]() ,
, ![]() 时,有
时,有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() 种情况;
种情况;
若![]() ,
, ![]() 分别在
分别在![]() 和
和![]() 内时,有下表
内时,有下表![]() 种情况.
种情况.
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
所以基本事件总数为![]() 种,而事件“
种,而事件“![]() ”所包含的基本事件个数有
”所包含的基本事件个数有![]() 种,
种,
所以![]() .
.
故从第一、五组中随机取出两个成绩,韧度存在明显差异的概率为![]() .
.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案【题目】某地区2009年至2015年农村居民家庭人均纯收入y(单位:千元)的数据如表:
年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2009年至2015年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2017年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为: 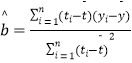 .
. ![]() .
.
参考数据:(﹣3)×(﹣1.4)+(﹣2)×(﹣1)+(﹣1)×(﹣0.7)+1×0.5+2×0.9+3×1.6=14.