题目内容
在三棱柱ABC-A1B1C1中,已知 BC=1,BB1=2,∠BAC=30°,∠BCC1=90°,AB⊥侧面BB1C1C,则直线C1B与侧面ACC1A1所成角的正弦值为________.
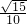
分析:以BA为x轴,以BC为y轴,以BB1为z轴,建立空间直角坐标系,由BC=1,BB1=2,∠BAC=30°,∠BCC1=90°,AB⊥侧面BB1C1C,知
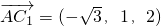 ,
,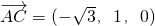 ,
,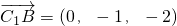 ,设面ACC1A1的法向量
,设面ACC1A1的法向量 ,则
,则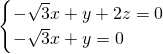 ,所以
,所以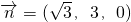 ,由此利用向量法能求出直线C1B与侧面ACC1A1所成角的正弦值.
,由此利用向量法能求出直线C1B与侧面ACC1A1所成角的正弦值.解答:
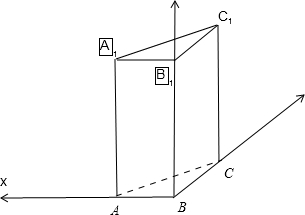 解:以BA为x轴,以BC为y轴,以BB1为z轴,建立如图所示的空间直角坐标系,
解:以BA为x轴,以BC为y轴,以BB1为z轴,建立如图所示的空间直角坐标系,∵BC=1,BB1=2,∠BAC=30°,∠BCC1=90°,AB⊥侧面BB1C1C,
∴A(
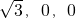 ),B(0,0,0),C(0,1,0),C1(0,1,2),
),B(0,0,0),C(0,1,0),C1(0,1,2),∴
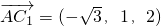 ,
,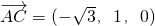 ,
,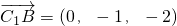 ,
,设面ACC1A1的法向量
 ,
,则
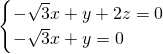 ,
,∴
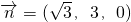 ,
,设直线C1B与侧面ACC1A1所成角为θ,
sinθ=|cos<
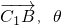 >|=|
>|=|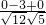 |=
|=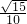 .
.故答案为:
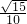 .
.点评:本题考查直线与平面所成角的正弦值的求法,解题时要认真审题,恰当地建立空间直角坐标系,注意向量法的合理运用.

练习册系列答案
相关题目
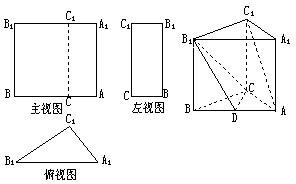 已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5,
已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5, 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
(2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.