题目内容
已知椭圆C: ,离心率
,离心率 ,O为坐标原点,A(a,0),B(0,b),点O到直线AB的距离为
,O为坐标原点,A(a,0),B(0,b),点O到直线AB的距离为
(1)求椭圆C的方程;
(2)过M(0,2)作倾斜角为锐角的直线l交椭圆C于不同的两点P,Q,若 =
=
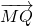 ,求直线l的方程.
,求直线l的方程.
 解:(1)∵A(a,0),B(0,b),
解:(1)∵A(a,0),B(0,b),∴直线AB的方程为
 ,即bx+ay-ab=0,
,即bx+ay-ab=0,∵点O到直线AB的距离为
 ,∴
,∴ ,①
,①∵离心率
 ,∴
,∴ ②
②联立①②得:a2=2,b2=1,
∴所求椭圆方程为:
 .
.(2)设P(x1,y1),Q(x2,y2),
∵M(0,2),
 =
=
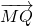 ,
,∴
 =(x1,y1-2),
=(x1,y1-2), ,
,设直线l的斜率为k,则直线l的方程为y=kx+2,
由
 ,得(2k2+1)x2+8kx+6=0,
,得(2k2+1)x2+8kx+6=0,∵直线l交椭圆C于不同的两点P,Q,
∴△=(8k)2-24(2k2+1)>0,解得
 .
. ,
, ,
,∵
 =
=
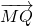 ,
, =(x1,y1-2),
=(x1,y1-2), ,
,∴
 ,
, =
= ,解得
,解得 ,
,∴直线l的倾斜角为锐角,∴k=
 ,
,∴直线l的方程为y=
 x+2.
x+2.分析:(1)由A(a,0),B(0,b),知直线AB的方程为bx+ay-ab=0,由点O到直线AB的距离为
 ,知
,知 ,再由
,再由 ,能求出椭圆方程.
,能求出椭圆方程.(2)设直线l的斜率为k,则直线l的方程为y=kx+2,由
 ,得(2k2+1)x2+8kx+6=0,设P(x1,y1),Q(x2,y2),
,得(2k2+1)x2+8kx+6=0,设P(x1,y1),Q(x2,y2), ,
, ,由M(0,2),
,由M(0,2), =
=
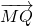 ,知
,知 =(x1,y1-2),
=(x1,y1-2), ,
, ,由此能求出直线l的方程.
,由此能求出直线l的方程.点评:本题考查椭圆方程的求法,考查直线方程的求法,解题时要认真审题,仔细解答,注意点到直线的距离公式和向量知识的合理运用.

练习册系列答案
相关题目
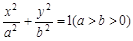 的离心率与等轴双曲线的离心率互为倒数,直线
的离心率与等轴双曲线的离心率互为倒数,直线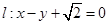 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切。
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切。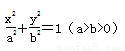 的离心率为
的离心率为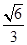 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为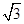 .
.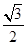 ,求△AOB面积的最大值.
,求△AOB面积的最大值. 的离心率为
的离心率为 ,椭圆C上任意一点到椭圆两个焦点的距离之和为6.
,椭圆C上任意一点到椭圆两个焦点的距离之和为6. :
: 与椭圆C交于
与椭圆C交于 ,
, 两点,点
两点,点 ,且
,且 ,求直线
,求直线