Question

（2009•闵行区二模）（理）在极坐标系中，两点的极坐标分别为A(2， 

π

3

)、B(1， -

π

3

)，O为极点，则△OAB面积为

3

2

．

Answer 1

分析：欲求△OAB的面积，根据极角可得三角形的内角∠AOB，由极径得边OA，OB的长，根据三角形的面积公式即可求得．

解答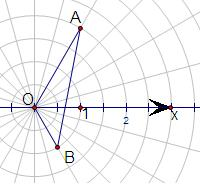：解：由极坐标的意义得：
△OAB的面积：

1

2

OA×OB×sin∠AOB=

1

2

×2×1×sin

2π

3

=

3

2

即：△OAB的面积：

3

2

．
故答案为：

3

2

．

点评：本题考查点的极坐标的应用，能在极坐标系中用极坐标刻画点的位置，体会在极坐标系和平面直角坐标系中刻画点的位置的区别．