题目内容
4.已知A(1,-4),B(-4,-2),C(-3,0),D(0,0),设AC与BD交于点P,求点P的坐标.分析 利用点斜式即可得出.
解答 解:直线AC的方程为:$y=\frac{4}{-3-1}(x+3)$,化为x+y+3=0;
直线DB的方程为:y=$\frac{-2}{-4}$x,化为x-2y=0.
点评 本题考查了点斜式,属于基础题.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
9.若α适合条件sin$\frac{α}{2}$=$\frac{1}{2}$($\sqrt{1+sinα}$+$\sqrt{1-sinα}$),则$\frac{α}{2}$的取值范围是( )
| A. | [2kπ,2kπ+$\frac{π}{2}$],k∈Z | B. | [2kπ+$\frac{π}{2}$,(2k+1)π],k∈Z | ||
| C. | [2kπ+$\frac{π}{4}$,2kπ+$\frac{3π}{4}$],k∈Z | D. | [2kπ+$\frac{3π}{4}$,2kπ+$\frac{5π}{4}$],k∈Z |
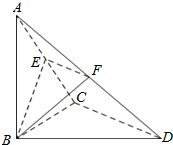 如图5,已知△BCD中,∠BCD=90°,BC=CD=1,AB=$\sqrt{6}$,AB⊥平面BCD,E、F分别是AC、AD的中点.
如图5,已知△BCD中,∠BCD=90°,BC=CD=1,AB=$\sqrt{6}$,AB⊥平面BCD,E、F分别是AC、AD的中点.