题目内容
若函数 满足
满足 且
且 时,
时,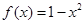 ,函数
,函数 分别在两相邻对称轴
分别在两相邻对称轴 与
与 处取得最值1与-1,则函数
处取得最值1与-1,则函数 在区间
在区间 内零点的个数为( )
内零点的个数为( )
| A.1006 | B.1007 | C.1008 | D.1010 |
C
解析试题分析: ,故
,故 周期为2,
周期为2, ,在同一坐标系内作出函数
,在同一坐标系内作出函数 与
与 的图象,利用函数
的图象,利用函数 的周期为4,数形结合即得交点个数为
的周期为4,数形结合即得交点个数为 ,故选C.
,故选C.
考点:1.函数图象;2.函数的周期性;3.函数零点.

练习册系列答案
相关题目
设函数 ,则
,则 是()
是()
| A.最小正周期为p的奇函数 | B.最小正周期为p的偶函数 |
C.最小正周期为 的奇函数 的奇函数 | D.最小正周期为 的偶函数 的偶函数 |
设S,T是R的两个非空子集,如果存在一个从S到T的函数y=f(x)满足:(i)T={f(x)|x∈S};(ii)对任意x1,x2∈S,当x1<x2时,恒有f(x1)<f(x2),那么称这两个集合“保序同构”,以下集合对不是“保序同构”的是( )
| A.A=N*,B=N |
| B.A={x|﹣1≤x≤3},B={x|x=﹣8或0<x≤10} |
| C.A={x|0<x<1},B=R |
| D.A=Z,B=Q |
下列函数,在其定义域内既是奇函数又是增函数的是 ( )
A.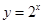  | B.  |
C.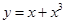  | D.  |
下列函数是偶函数,且在 上单调递增的是( )
上单调递增的是( )
A. | B. | C. | D. |
已知 是
是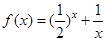 的一个零点,
的一个零点, ,则 ( )
,则 ( )
A. | B. |
C. | D. |
函数f(x)=tan(2x-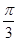 )的单调递增区间是()
)的单调递增区间是()
A.[ , , ](k∈Z) ](k∈Z) |
B.( , , )(k∈Z) )(k∈Z) |
C.[ , , ](k∈Z) ](k∈Z) |
D.( , , )(k∈Z) )(k∈Z) |
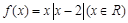 ,若存在正实数k,使得方程
,若存在正实数k,使得方程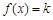 在区间
在区间 上有三个互不相等的实数根
上有三个互不相等的实数根 ,则x1+x2+x3的取值范围是 ( )
,则x1+x2+x3的取值范围是 ( )


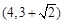
 ”:
”: ,设函数
,设函数 .若函数
.若函数 的图象与x轴恰好有两个共公点,则实数c的取值范围是( )
的图象与x轴恰好有两个共公点,则实数c的取值范围是( )


