题目内容
若定义在R上的函数f(x)满足f(-x)="f(x)," f(2-x)=f(x),且当x∈[0,1]时,其图象是四分之一圆(如图所示),则函数H(x)= |xex|-f(x)在区间[-3,1]上的零点个数为 ( )
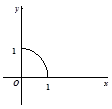
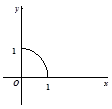

| A.5 | B.4 | C.3 | D.2 |
B
试题分析:因为定义在R上的函数f(x)满足f(-x)=f(x),所以函数
 为偶函数,又因为f(2-x)=f(x),所以函数
为偶函数,又因为f(2-x)=f(x),所以函数 关于直线
关于直线 对称.因为函数H(x)= |xex|-f(x)在区间[-3,1]上的零点即等价求方程
对称.因为函数H(x)= |xex|-f(x)在区间[-3,1]上的零点即等价求方程 的解的个数.等价于函数
的解的个数.等价于函数 和函数
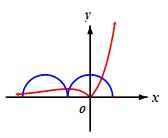
和函数 的图像的交点个数,由图象可得共有4个交点.故选B.
的图像的交点个数,由图象可得共有4个交点.故选B.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 )x-
)x- 的零点,则x0属于区间( )
的零点,则x0属于区间( ) 的图像过点
的图像过点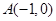 和
和 ,则下列各点在函数
,则下列各点在函数

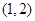

 ,则当x∈(-∞,-2)时,f(x)的解析式为( )
,则当x∈(-∞,-2)时,f(x)的解析式为( )

 +
+ 的最小值为________.
的最小值为________. 的图象过原点,且关于点(-1,2)成中心对称.
的图象过原点,且关于点(-1,2)成中心对称. 为等比数列,并求出数列{an}的通项公式.
为等比数列,并求出数列{an}的通项公式.