题目内容
已知a,b,c均为正数,证明:a2+b2+c2+(| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 3 |
分析:两次运用基本不等式即可证明结论.
解答:证明:∵a,b,c均为正数,
∴左边≥3
+(3
)2≥2
=2
=6
,
当且仅当a=b=c时取等号,
∴a2+b2+c2+(
+
+
)2≥6
.
∴左边≥3
| 3 | a2b2c2 |
| 3 |
| ||
3
|
| 27 |
| 3 |
当且仅当a=b=c时取等号,
∴a2+b2+c2+(
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 3 |
点评:本题考查基本不等式的运用,考查学生分析解决问题的能力,正确运用基本不等式是关键.

练习册系列答案
相关题目
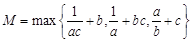 ,则M的最小值为 .
,则M的最小值为 .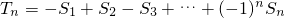 ,求满足不等式
,求满足不等式 的所有n的值;
的所有n的值;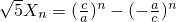 (n∈N+),证明:数列{
(n∈N+),证明:数列{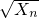 }中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.
}中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.