题目内容
12．已知△ABC中，A（0，3），B（2，-1），P、Q分别为AC、BC的中点，则直线PQ的斜率为-2．分析 先求出直线PQ是△ABC的中位线，从而得到KPQ=KAB，求出直线的斜率即可．
解答 解：∵P、Q分别为AC、BC的中点，
∴PQ是△ABC的中位线，
∴PQ∥AB，
∴KPQ=KAB=$\frac{-1-3}{2-0}$=-2，
故答案为：-2．
点评 本题考察了求直线的斜率问题，考察三角形的中位线问题，是一道基础题．
练习册系列答案
相关题目
19．已知空间向量$\overrightarrow{AB}$，$\overrightarrow{BC}$，$\overrightarrow{CD}$，$\overrightarrow{AD}$，则下列结论正确的是（ ）
| A． | $\overrightarrow{AB}$=$\overrightarrow{BC}$+$\overrightarrow{CD}$ | B． | $\overrightarrow{AB}$-$\overrightarrow{DC}$+$\overrightarrow{BC}$=$\overrightarrow{AD}$ | C． | $\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{DC}$ | D． | $\overrightarrow{BC}$=$\overrightarrow{BD}$-$\overrightarrow{DC}$ |
7．
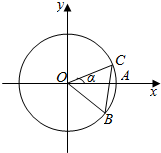如图，圆O与x轴的正半轴的交点为A，点C、B在圆O上，且点C位于第一象限，点B的坐标为（$\frac{12}{13}$，-$\frac{5}{13}$），∠AOC=α，若|BC|=1，则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为（ ）
如图，圆O与x轴的正半轴的交点为A，点C、B在圆O上，且点C位于第一象限，点B的坐标为（$\frac{12}{13}$，-$\frac{5}{13}$），∠AOC=α，若|BC|=1，则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为（ ）| A． | $\frac{5}{13}$ | B． | $\frac{12}{13}$ | C． | -$\frac{5}{13}$ | D． | -$\frac{12}{13}$ |
17．已知函数f（x）的图象如图：则满足f（2x）•f（lg（x2-6x+120））≤0的x的取值范围是（ ）
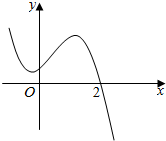
| A． | （-∞，1] | B． | [1，+∞） | C． | [0，+∞） | D． | （-∞，2] |
1．已知不共线向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{AB}$=t$\overrightarrow{a}$-$\overrightarrow{b}$（t∈R），$\overrightarrow{AC}$=2$\overrightarrow{a}$+3$\overrightarrow{b}$，若A，B，C三点共线，则实数t=（ ）
| A． | -$\frac{1}{3}$ | B． | -$\frac{2}{3}$ | C． | $\frac{3}{2}$ | D． | -$\frac{3}{2}$ |