题目内容
如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线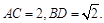 AE、CF都与平面ABCD垂直,AE=1,CF=2.
AE、CF都与平面ABCD垂直,AE=1,CF=2.
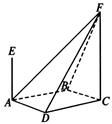
(1)求二面角B-AF-D的大小;
(2)求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积.
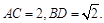 AE、CF都与平面ABCD垂直,AE=1,CF=2.
AE、CF都与平面ABCD垂直,AE=1,CF=2.
(1)求二面角B-AF-D的大小;
(2)求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积.
(1) (2)
(2)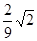 .
.
 (2)
(2)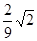 .
.试题分析:(1)方法一:连接
 交于菱形的中心
交于菱形的中心 ,过
,过 作
作 ,
,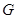 为垂足,连接
为垂足,连接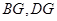 ,根据定义可知
,根据定义可知 为二面角
为二面角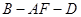 的平面角,在三角形
的平面角,在三角形 中求出此角即可;
中求出此角即可;方法二:设
 与
与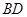 交点为
交点为 ,以
,以 为坐标原点,分别以
为坐标原点,分别以 所在直线为
所在直线为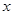 轴
轴 轴建立如图所示的空间直角坐标系, 设平面
轴建立如图所示的空间直角坐标系, 设平面 ,平面
,平面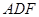 的法向量分别为
的法向量分别为 ,利用
,利用 的公式进行计算.
的公式进行计算.(2)连接
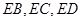 ,设直线
,设直线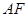 与直线
与直线 相交于点
相交于点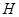 ,则四棱锥
,则四棱锥 与四棱锥
与四棱锥 的公共部分为四棱锥
的公共部分为四棱锥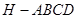 ,过
,过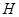 作
作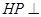 平面
平面 ,
,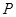 为垂足,然后求出
为垂足,然后求出 ,利用体积公式
,利用体积公式 求解即可.
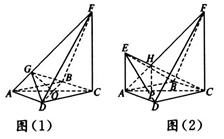
求解即可.试题解析:(1)方法一:如图(1)连结AC、BD交于菱形的中心O,过O
作OG⊥AF,G为垂足. 连结BG、DG.
由BD⊥AC,BD⊥CF,得BD⊥平面ACF, 故BD⊥AF. 于是AF⊥平面BGD,
所以BG⊥AF,DG⊥AF,∠BGD为二面角B-AF-D的平面角. 3分
由FC⊥AC,FC=AC=2,得∠FAC
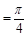 ,
, .
.由OB⊥OG,OB=OD=
 ,得∠BGD=2∠BGO
,得∠BGD=2∠BGO .
.即二面角B-AF-D的大小为
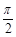 . 6分
. 6分
方法二:设AC与BD交点为O,以O为坐标原点,分别以BD 、AC所在直线为x轴
y轴建立如图所示的空间直角坐标系
则A(0,-1,0),B(
 ,0,0),D(
,0,0),D( ,0,0),F(0,1,2)
,0,0),F(0,1,2) ,
, ,
,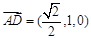 2分
2分设平面ABF,平面ADF的法向量分别为

设

由
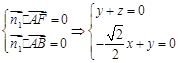
令
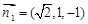 4分
4分同理可得
 ∴
∴ ∴
∴
∴二面角B-AF-D的大小为
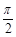 6分
6分(2)如图(2)连EB、EC、ED,设直线AF与直线CE相交于点H,
则四棱锥E-ABCD与四棱锥F-ABCD的公共部分为四棱锥H-ABCD.
过H作HP⊥平面ABCD,所以平面ACFE⊥平面ABCD,
从而
 . 7分
. 7分由
 ,得
,得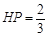 . 9分
. 9分又因为
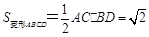
故四棱锥
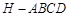 的体积
的体积 . 12分
. 12分
练习册系列答案
相关题目
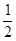
 ,则它的侧棱和底面所成角= .
,则它的侧棱和底面所成角= . 的侧棱
的侧棱 、
、 、
、 两两垂直,且
两两垂直,且 ,则正三棱锥
,则正三棱锥 的外接球的表面积是 .
的外接球的表面积是 .




 、
、 是半径为
是半径为 的球
的球 的球面上两点,它们的球面距离为
的球面上两点,它们的球面距离为 ,求过
,求过







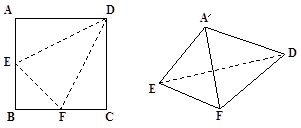
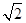
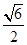
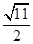
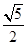
 的棱长为1,线段
的棱长为1,线段 上有两个动点E,、F,且
上有两个动点E,、F,且 ,则下列结论中错误的是( )
,则下列结论中错误的是( )


 的体积为定值
的体积为定值 的面积与
的面积与 的面积相等
的面积相等