题目内容
设函数f(x)=ax3+bx2+cx+2的导函数为f′(x),如果f′(x)为偶函数,则一定有( )
|
| A. | a≠0,c=0 | B. | a=0,c≠0 | C. | b=0 | D. | b=0,c=0 |
C解:函数f(x)=ax3+bx2+cx+2的导函数为f′(x)=3ax2+2bx+c,∵函数f′(x)=3ax2+2bx+c是定义在R上的偶函数,∴f'(x)=f'(﹣x),即3ax2+2bx+c=3ax2﹣2bx+c,∴2bx=0恒成立,b=0.故选C.

练习册系列答案
相关题目
已知函数 是奇函数,则
是奇函数,则 =( )
=( )
|
| A. |
| B. |
| C. | 2 | D. | ﹣2 |
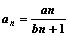 ,其中a、b均为正常数,那么数列{an}的单调性为( )
,其中a、b均为正常数,那么数列{an}的单调性为( ) 、
、 都是定义在R上的函数,
都是定义在R上的函数, ,且
,且 ,
, 若数列
若数列 的前n项和大于62,则n的最小值为
的前n项和大于62,则n的最小值为

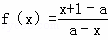 ,定义域为A.(1)试证明y=f(x)的图象关于点(a,﹣1)成中心对称;
,定义域为A.(1)试证明y=f(x)的图象关于点(a,﹣1)成中心对称;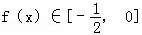 ;(3)对于给定的x1∈A,设计构造过程:x2=f(x1),x3=f(x2),…,xn+1=f(xn).如果xi∈A(i=2,3,4…),构造过程将继续下去;如果xi∉A,构造过程将停止.若对任意x1∈A,构造过程都可以无限进行下去,求a的值.
;(3)对于给定的x1∈A,设计构造过程:x2=f(x1),x3=f(x2),…,xn+1=f(xn).如果xi∈A(i=2,3,4…),构造过程将继续下去;如果xi∉A,构造过程将停止.若对任意x1∈A,构造过程都可以无限进行下去,求a的值.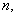 若
若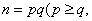 且
且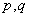 为整数),当
为整数),当 最小时,则称
最小时,则称 为
为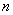 的“最佳分解”,并规定
的“最佳分解”,并规定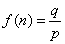 (如12的分解有
(如12的分解有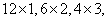 其中,
其中,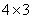 为12的最佳分解,则
为12的最佳分解,则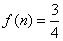 )。关于
)。关于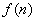 有下列判断:①
有下列判断:①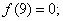 ②
②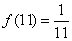 ;③
;③ ④
④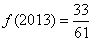 。其中,正确判断的序号是 .
。其中,正确判断的序号是 . 与实数m的一种符号运算为m⊙
与实数m的一种符号运算为m⊙ 已知函数
已知函数 g(x)=4⊙
g(x)=4⊙ (1) 求g(x)的单调区间;
(1) 求g(x)的单调区间; 上
上 >2a-3恒成立,求a的取值范围。
>2a-3恒成立,求a的取值范围。 ,当
,当 ,
, 时,
时, ,若在区间
,若在区间 ,
, 有两个零点,则实数
有两个零点,则实数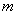 的取值范围是 ( )
的取值范围是 ( ) .
. ,
,
 .
. ,
,
 .
.
 .
. ,
,
 的定义域是
的定义域是 ,且
,且 ,当
,当 时,
时, ,(1)求证:
,(1)求证: 上的解析式;
上的解析式;