题目内容
曲线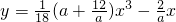 在点x=1处的切线为m,在点x=0处的切线为n,则直线m与n的夹角的取值范围是
在点x=1处的切线为m,在点x=0处的切线为n,则直线m与n的夹角的取值范围是
- A.
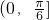
- B.

- C.
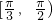
- D.
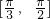
C
分析:先根据导数的几何意义利用导数求出曲线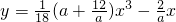 在点x=1处的切线斜率,再设直线m与n的夹角为θ,结合两直线的夹角公式求得夹角的正切值,最后利用基本不等式求正切值的取值范围即可得出直线m与n的夹角的取值范围.
在点x=1处的切线斜率,再设直线m与n的夹角为θ,结合两直线的夹角公式求得夹角的正切值,最后利用基本不等式求正切值的取值范围即可得出直线m与n的夹角的取值范围.
解答:∵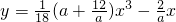 ,
,
∴ ,
,
∴曲线 在点x=1处的切线斜率为:
在点x=1处的切线斜率为:
k1= ,
,
在点x=0处的切线为k2= ,
,
设直线m与n的夹角为θ,则:
tanθ= =|
=| |≥
|≥ ,
,
则直线m与n的夹角的取值范围是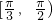 ,
,
故选C.
点评:本小题主要考查利用导数研究曲线上某点切线方程、两直线的夹角与到角问题等基础知识,考查运算求解能力,化归与转化思想.属于基础题.
分析:先根据导数的几何意义利用导数求出曲线
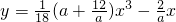 在点x=1处的切线斜率,再设直线m与n的夹角为θ,结合两直线的夹角公式求得夹角的正切值,最后利用基本不等式求正切值的取值范围即可得出直线m与n的夹角的取值范围.
在点x=1处的切线斜率,再设直线m与n的夹角为θ,结合两直线的夹角公式求得夹角的正切值,最后利用基本不等式求正切值的取值范围即可得出直线m与n的夹角的取值范围.解答:∵
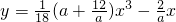 ,
,∴
 ,
,∴曲线
 在点x=1处的切线斜率为:
在点x=1处的切线斜率为:k1=
 ,
,在点x=0处的切线为k2=
 ,
,设直线m与n的夹角为θ,则:
tanθ=
 =|
=| |≥
|≥ ,
,则直线m与n的夹角的取值范围是
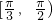 ,
,故选C.
点评:本小题主要考查利用导数研究曲线上某点切线方程、两直线的夹角与到角问题等基础知识,考查运算求解能力,化归与转化思想.属于基础题.

练习册系列答案
相关题目
 =x+ax2+blnx,曲线y=
=x+ax2+blnx,曲线y= =x+ax2+blnx,曲线y =
=x+ax2+blnx,曲线y = =x+ax2+blnx,曲线y=
=x+ax2+blnx,曲线y=