题目内容
甲、乙两人独立地破译1个密码,他们能译出密码的概率分别为![]() 和
和![]() .
.
求:(1)有且只有甲一人译出密码的概率;
(2)甲和乙至多有一人译出密码的概率;
(3)若要使译出密码的概率不小于![]() ,而且全用像乙这样的人,问至少需要多少人?
,而且全用像乙这样的人,问至少需要多少人?
解:记“甲译出密码”为事件A,“甲译不出密码”为事件![]() ;“乙译出密码”为事件B,“乙译不出密码”为事件
;“乙译出密码”为事件B,“乙译不出密码”为事件![]() .
.
(1)“有且只有甲一人译出密码”为事件A1,则由于甲、乙两人独立地破译密码,为相互独立事件,所以事件A1发生是指事件A和B同时发生,从而有P(A1)=P(A·![]() )=P(A)·P(
)=P(A)·P(![]() )=
)=![]() ×(1-
×(1-![]() )=
)=![]() .
.
(2)“甲和乙至多有一人译出密码”为事件A2,则事件![]() 的对立事件是“甲、乙两人都译出密码”,即A2=A·B.从而有P(A2)=1-P(
的对立事件是“甲、乙两人都译出密码”,即A2=A·B.从而有P(A2)=1-P(![]() )=1-P(A·B)=1-P(A)·P(B)=1-
)=1-P(A·B)=1-P(A)·P(B)=1-![]() ×
×![]() =
=![]() .
.
(3)设至少需要n个人,则由于n个像乙这样的人都译不出密码的概率为(1-![]() )n,根据题意,得n个像乙这样的人译出密码的概率满足1-(1-
)n,根据题意,得n个像乙这样的人译出密码的概率满足1-(1-![]() )n≥
)n≥![]() ,即3n≥100(n∈N*).
,即3n≥100(n∈N*).
解得n≥5,且n∈N*.因此需要像乙这样的人至少5人.

练习册系列答案
相关题目
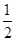 和
和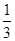 , 求:
, 求: