题目内容
甲、乙两人独立地破译1个密码,他们能译出密码的概率分别为| 1 |
| 3 |
| 1 |
| 4 |
(1)恰有1人译出密码的概率;
(2)若达到译出密码的概率为
| 99 |
| 100 |
分析:(1)恰有1人译出密码的概率为 P(A•
)+P(
•B)=
×
+
×
,运算求得结果.
(2)先求出n个乙这样的人都译不出密码的概率为 (1-
)n,由 1-(1-
)n≥
可得 n 的范围,即得所求.
. |
| B |
. |
| A |
| 1 |
| 3 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 4 |
(2)先求出n个乙这样的人都译不出密码的概率为 (1-
| 1 |
| 4 |
| 1 |
| 4 |
| 99 |
| 100 |
解答:解:设“甲译出密码”为事件A;“乙译出密码”为事件B,
则 P(A)=
,P(B)=
.
(1)P(A•
)+P(
•B)=
×
+
×
=
.
(2)n个乙这样的人都译不出密码的概率为 (1-
)n,由 1-(1-
)n≥
可得 n≥17,
达到译出密码的概率为
,至少需要17 人.
则 P(A)=
| 1 |
| 3 |
| 1 |
| 4 |
(1)P(A•
. |
| B |
. |
| A |
| 1 |
| 3 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 4 |
| 5 |
| 12 |
(2)n个乙这样的人都译不出密码的概率为 (1-
| 1 |
| 4 |
| 1 |
| 4 |
| 99 |
| 100 |
达到译出密码的概率为
| 99 |
| 100 |
点评:本题考查n次独立重复实验中恰好发生k次的概率,等可能事件的概率,所求的事件与它的对立事件概率间的关系,求出
n个乙这样的人都译不出密码的概率,是解题的关键.
n个乙这样的人都译不出密码的概率,是解题的关键.

练习册系列答案
相关题目
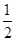 和
和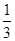 , 求:
, 求: