题目内容
关于函数f(x)=4sin(πx+ ),x∈R,有下列命题:
),x∈R,有下列命题:①对任意x∈R,有f(x+1)=-f(x)成立;
②y=f(x)在区间[0,1]上的最小值为-4;
③y=f(x)的图象关于点(-
 ,0)对称;
,0)对称;④y=f(x)的图象关于直线x=
 对称.
对称.其中正确的命题的序号是 .(注:把你认为正确的命题的序号都填上.)
【答案】分析:利用诱导公式化简f(x+1)的解析式,可得①正确.
根据 ≤πx+
≤πx+ ≤
≤ ,得πx+
,得πx+ =
= 时,f(x)有最小值为 4×(-
时,f(x)有最小值为 4×(- )=-2
)=-2 ,可得②不正确.
,可得②不正确.
由点(- ,0)是f(x)与x轴的交点,可得③正确.
,0)是f(x)与x轴的交点,可得③正确.
由当x= 时,f(x)=sin
时,f(x)=sin ≠±1,故x=
≠±1,故x= 不是函数的对称轴,可得④不正确.
不是函数的对称轴,可得④不正确.
解答:解:f(x+1)=4sin(π+πx+ )=-4sin(πx+
)=-4sin(πx+ )=-f(x),故①正确.
)=-f(x),故①正确.
在区间[0,1]上, ≤πx+
≤πx+ ≤
≤ ,故πx+
,故πx+ =
= 时,f(x)有最小值为 4×(-
时,f(x)有最小值为 4×(- )=-2
)=-2 ,故②不正确.
,故②不正确.
当x=- 时,f(x)=sin0=0,故点(-
时,f(x)=sin0=0,故点(- ,0)是f(x)与x轴的交点,故y=f(x)的图象关于点(-
,0)是f(x)与x轴的交点,故y=f(x)的图象关于点(- ,0)对称,故③正确.
,0)对称,故③正确.
当x= 时,f(x)=sin
时,f(x)=sin ≠±1,故x=
≠±1,故x= 不是函数的对称轴,故④不正确.
不是函数的对称轴,故④不正确.
故答案为 ①③.
点评:本题考查正弦函数的对称性以及最值,诱导公式的应用,明确对称中心、对称轴的定义、函数取最值的条件,是解题的关键.
根据
 ≤πx+
≤πx+ ≤
≤ ,得πx+
,得πx+ =
= 时,f(x)有最小值为 4×(-
时,f(x)有最小值为 4×(- )=-2
)=-2 ,可得②不正确.
,可得②不正确.由点(-
 ,0)是f(x)与x轴的交点,可得③正确.
,0)是f(x)与x轴的交点,可得③正确.由当x=
 时,f(x)=sin
时,f(x)=sin ≠±1,故x=
≠±1,故x= 不是函数的对称轴,可得④不正确.
不是函数的对称轴,可得④不正确.解答:解:f(x+1)=4sin(π+πx+
 )=-4sin(πx+
)=-4sin(πx+ )=-f(x),故①正确.
)=-f(x),故①正确.在区间[0,1]上,
 ≤πx+
≤πx+ ≤
≤ ,故πx+
,故πx+ =
= 时,f(x)有最小值为 4×(-
时,f(x)有最小值为 4×(- )=-2
)=-2 ,故②不正确.
,故②不正确.当x=-
 时,f(x)=sin0=0,故点(-
时,f(x)=sin0=0,故点(- ,0)是f(x)与x轴的交点,故y=f(x)的图象关于点(-
,0)是f(x)与x轴的交点,故y=f(x)的图象关于点(- ,0)对称,故③正确.
,0)对称,故③正确.当x=
 时,f(x)=sin
时,f(x)=sin ≠±1,故x=
≠±1,故x= 不是函数的对称轴,故④不正确.
不是函数的对称轴,故④不正确.故答案为 ①③.
点评:本题考查正弦函数的对称性以及最值,诱导公式的应用,明确对称中心、对称轴的定义、函数取最值的条件,是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 )(
)( ),有下列命题:
),有下列命题: 可得
可得 必是
必是 的整数倍;
的整数倍;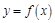 的表达式可改写为
的表达式可改写为 ;
; 对称;
对称; 对称.
对称.