题目内容
已知函数f(x)=x3+ax2+bx在x=1处有极值-2.(1)求常数a、b;
(2)求曲线y=f(x)与x轴所包围的面积.
【答案】分析:(1)求导函数,利用函数f(x)=x3+ax2+bx在x=1处有极值-2,建立方程组,即可求得a,b的值;
(2)确定函数的积分区间,被积函数,再求出原函数,即可求得结论.
解答:解:(1)f′(x)=3x2+2ax+b,由f(1)=-2及f′(1)=0得: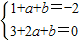 ,解得
,解得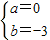 ;
;
(2)由(1)知f(x)=x3-3x=x(x+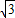 )(x-
)(x-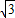 )
)
∴当x<-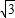 或0<x<
或0<x<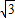 时,f(x)<0,当-
时,f(x)<0,当-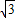 <x<0或x>
<x<0或x>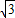 时,f(x)>0,
时,f(x)>0,
∴曲线y=f(x)与x轴所包围的面积: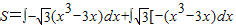 =
=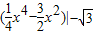 -
-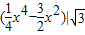 =
= .
.
点评:本题考查导数知识的运用,考查函数的极值,考查利用定积分求面积,正确求导是关键.
(2)确定函数的积分区间,被积函数,再求出原函数,即可求得结论.
解答:解:(1)f′(x)=3x2+2ax+b,由f(1)=-2及f′(1)=0得:
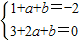 ,解得
,解得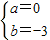 ;
;(2)由(1)知f(x)=x3-3x=x(x+
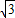 )(x-
)(x-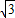 )
) ∴当x<-
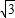 或0<x<
或0<x<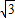 时,f(x)<0,当-
时,f(x)<0,当-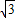 <x<0或x>
<x<0或x>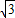 时,f(x)>0,
时,f(x)>0,∴曲线y=f(x)与x轴所包围的面积:
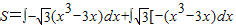 =
=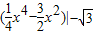 -
-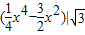 =
= .
.点评:本题考查导数知识的运用,考查函数的极值,考查利用定积分求面积,正确求导是关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|