题目内容
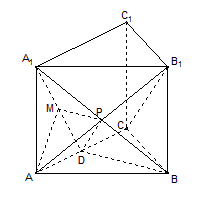
如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是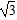 ,D是AC的中点。
,D是AC的中点。
(1)求证:B1C∥平面A1BD;
(2)求二面角A1-BD-A的大小;
(3)求直线AB1与平面A1BD所成的角的正弦值。
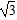 ,D是AC的中点。
,D是AC的中点。 (1)求证:B1C∥平面A1BD;
(2)求二面角A1-BD-A的大小;
(3)求直线AB1与平面A1BD所成的角的正弦值。
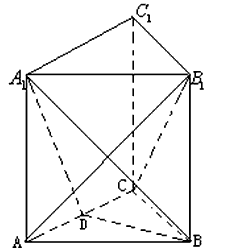
| 解:(1)设AB1与A1B相交于点P,连接PD,则P为AB1中点, ∵D为AC中点, ∴PD∥B1C, 又∵PD 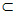 平面A1BD, 平面A1BD,∴B1C∥平面A1BD; (2)∵正三棱住ABC-A1B1C1, ∴AA1⊥底面ABC, 又∵BD⊥AC, ∴A1D⊥BD, ∴∠A1DA就是二面角A1-BD-A的平面角, ∵AA1= 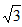 ,AD= ,AD=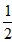 AC=1, AC=1,∴tan∠A1DA= 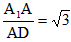 , ,∴∠A1DA= 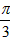 ,即二面角A1-BD-A的大小是 ,即二面角A1-BD-A的大小是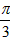 ; ;(3)由(2)作AM⊥A1D,M为垂足, ∵BD⊥AC,平面A1ACC1⊥平面ABC, 平面A1ACC1∩平面ABC=AC, ∴BD⊥平面A1ACC1, ∵AM 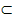 平面A1ACC1, 平面A1ACC1,∴BD⊥AM, ∵A1D∩BD=D, ∴AM⊥平面A1DB,连接MP, 则∠APM就是直线A1B与平面A1BD所成的角, ∵AA1= 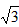 ,AD=1, ,AD=1,∴在Rt△AA1D中,∠A1DA= 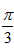 , ,∴AM=1×sin60°= 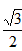 ,AP= ,AP=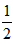 AB1= AB1=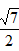 , ,∴sin∠APM= 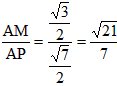 , ,∴直线AB1与平面A1BD所成的角的正弦值为 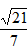 。 。 |
 |

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目

 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC. (2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC= 如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB
如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=