题目内容
已知函数 ,
,  .
.
(Ⅰ)如果函数 在
在 上是单调函数,求
上是单调函数,求 的取值范围;
的取值范围;
(Ⅱ)是否存在正实数 ,使得函数
,使得函数 在区间
在区间 内有两个不同的零点?若存在,请求出
内有两个不同的零点?若存在,请求出 的取值范围;若不存在,请说明理由
的取值范围;若不存在,请说明理由
【答案】
Ⅰ)当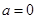 时,
时,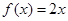 ,符合题意.---------1分
,符合题意.---------1分
当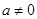 时,
时,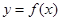 的对称轴方程为
的对称轴方程为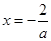 ,-------2分
,-------2分
由于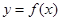 在
在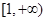 上是单调函数,所以
上是单调函数,所以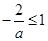 ,解得
,解得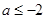 或
或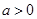 ,
,
综上,a的取值范围是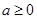 ,或
,或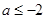 . …………………………4分
. …………………………4分
(Ⅱ)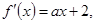
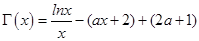 ,---------5分
,---------5分
因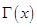 在区间(
在区间(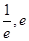 )内有两个不同的零点,所以
)内有两个不同的零点,所以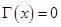 ,
,
即方程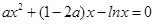 在区间(
在区间(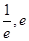 )内有两个不同的实根. …………6分
)内有两个不同的实根. …………6分
设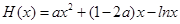
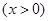 ,
,
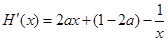
 ………7分
………7分
令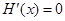 ,因为为正数,解得
,因为为正数,解得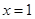 或
或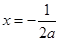 (舍)
(舍)
当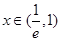 时,
时, 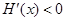 ,
,
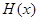 是减函数;
是减函数;
当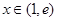 时,
时, 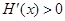 ,
,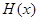 是增函数. …………………………8分
是增函数. …………………………8分
为满足题意,只需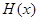 在(
在(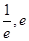 )内有两个不相等的零点, 故
)内有两个不相等的零点, 故
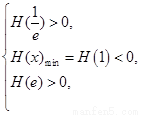 解得
解得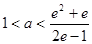
【解析】(I)本题转化为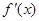 在
在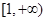 上恒小于等于零或恒大于等于零.
上恒小于等于零或恒大于等于零.
(II)求出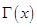 的解析式,然后研究其在区间
的解析式,然后研究其在区间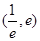 内的单调性和极值,画出其画图,数形结合求解.
内的单调性和极值,画出其画图,数形结合求解.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|