题目内容
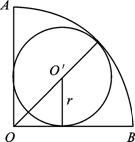
如下图，扇形AOB的半径为1，中心角为60°，PQRS是扇形的内接矩形.问P在什么位置时，矩形PQRS的面积最大？试求出这个最大值.
解:连结OP，设∠AOP=x,则PS=sinx，RS=cosx-sinx·cot60°.
∴S=(cosx-sinx·cot60°)·sinx
=
sin2x-
sin2x=
sin2x-
·
=
sin2x+
cos2x-
=
(
sin2x+
cos2x)-
=
·sin(2x+30°)- 
.
∵x∈(0°,60°),∴2x+30°∈(30°,150°).
∴当2x+30°=90°，x=30°,即点P在的中点时,Smax=
-
=
.
练习册系列答案
相关题目
=100π m)
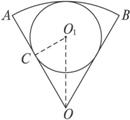
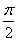的扇形（如下图扇形AOB所示,其中OA=10米）.为了节约能源，提倡低碳，学校计划在第一学术厅房顶平面上水平铺设世博会专用的太阳能屋面(形状如下图矩形阴影部分所示,矩形DOEC的邻边OD、OE分别在OA、OB上,动点C在
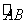上),请问动点C在