题目内容
如下图，
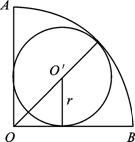
在扇形AOB中，∠AOB=90°，弧AB长为l，求此扇形内切圆的面积.
解析：∵弧AB长为l，∠AOB=
，
∴OA=
=(
+1)r.
∴r=
(
-1).
∴S=πr2=
l2.
练习册系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
教育世家状元卷系列答案黄冈课堂作业本系列答案单元加期末复习先锋大考卷系列答案题目内容
如下图，
在扇形AOB中，∠AOB=90°，弧AB长为l，求此扇形内切圆的面积.
解析：∵弧AB长为l，∠AOB=，
∴OA==(+1)r.
∴r=(-1).
∴S=πr2= l2.
教育世家状元卷系列答案黄冈课堂作业本系列答案单元加期末复习先锋大考卷系列答案
=100π m)
的扇形（如下图扇形AOB所示,其中OA=10米）.为了节约能源，提倡低碳，学校计划在第一学术厅房顶平面上水平铺设世博会专用的太阳能屋面(形状如下图矩形阴影部分所示,矩形DOEC的邻边OD、OE分别在OA、OB上,动点C在
上),请问动点C在