题目内容
设A(-c,0)、B(c,0)(c>0)为两定点,动点P到A点的距离与到B点的距离的比为定值a(a>0),求P点的轨迹.
解析:设动点P的坐标为(x,y),由![]() =a(a>0),得
=a(a>0),得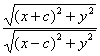 =a,
=a,
化简得(1-a2)x2+2c(1+a2)x+c2(1-a2)+(1-a2)y2=0,
当a≠1时,得x2+![]() cx+c2+y2=0.
cx+c2+y2=0.
整理得(x-![]() c)2+y2=(
c)2+y2=(![]() )2.
)2.
当a=1时,化简得x=0,
故当a≠1时,P点的轨迹是以(![]() c,0)为圆心,以|
c,0)为圆心,以|![]() |为半径的圆;当a=1时,P点的轨迹是y轴.
|为半径的圆;当a=1时,P点的轨迹是y轴.

练习册系列答案
相关题目
函数f(x)在定义域R内可导,若f(x)=f(2-x),且当x∈(-∞,1)时,(x-1)f′(x)<0,设a=f(0),b=f(
),c=f(3),则( )
| 1 |
| 2 |
| A、a<b<c |
| B、c<a<b |
| C、c<b<a |
| D、b<c<a |
 ),c=f(3),则( )
),c=f(3),则( ) ),c=f(3),则( )
),c=f(3),则( )