题目内容
已知函数f（x）=
x3+
ax2+2bx+c（a，b，c∈R），且函数f（x）在区间（0，1）内取得极大值，在区间（1，2）内取得极小值，则z=（a+3）2+b2的取值范围（ ）A．（
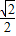，2）B．（
，4）C．（1，2）
D．（1，4）
【答案】分析：据极大值点左边导数为正右边导数为负，极小值点左边导数为负右边导数为正得a，b的约束条件，据线性规划求出最值．
解答：解：∵f（x）=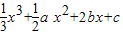
∴f′（x）=x2+ax+2b
∵函数f（x）在区间（0，1）内取得极大值，在区间（1，2）内取得极小值
∴f′（x）=x2+ax+2b=0在（0，1）和（1，2）内各有一个根
f′（0）＞0，f′（1）＜0，f′（2）＞0
即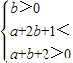
（a+3）2+b2表示点（a，b）到点（-3，0）的距离的平方，
由图知（-3，0）到直线a+b+2=0的距离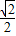
，平方为
为最小值，
（-3，0）与（-1，0）的距离2，平方为4为最大值
故选项为B
点评：本题考查函数极值存在条件及线性规划求最值．
解答：解：∵f（x）=
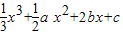
∴f′（x）=x2+ax+2b
∵函数f（x）在区间（0，1）内取得极大值，在区间（1，2）内取得极小值
∴f′（x）=x2+ax+2b=0在（0，1）和（1，2）内各有一个根
f′（0）＞0，f′（1）＜0，f′（2）＞0
即
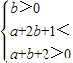
（a+3）2+b2表示点（a，b）到点（-3，0）的距离的平方，
由图知（-3，0）到直线a+b+2=0的距离
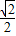，平方为为最小值，（-3，0）与（-1，0）的距离2，平方为4为最大值
故选项为B
点评：本题考查函数极值存在条件及线性规划求最值．
练习册系列答案
长江作业本同步练习册系列答案
小天才课时作业系列答案
一课四练系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|