题目内容

设函数f（x）=msinx+cosx（x∈R）的图象经过点(
π
2
，1)．
（Ⅰ）求y=f（x）的解析式，并求函数的最小正周期和最值．
（Ⅱ）若f(
π
12
)=
2
sinA，其中A是面积为
3
3
2
的锐角△ABC的内角，且AB=2，求AC和BC的长．
（Ⅰ）∵函数f（x）=msinx+cosx（x∈R）的图象经过点(
π
2
，1)，
∴msin
π
2
+cos
π
2
=1，
∴m=1，（2分）
∴f(x)=sinx+cosx=
2
sin(x+
π
4
)．（4分）
∴函数的最小正周期T=2π．（5分）
当x=
π
4
+2kπ(k∈Z)时，f（x）的最大值为
2
，当x=
5π
4
+2kπ(k∈Z)时，f（x）最小值为-
2
．（7分）
（Ⅱ）因为f(
π
12
)=
2
sinA，即f(
π
12
)=
2
sin
π
3
=
2
sinA，
∴sinA=sin
π
3
，
∵A是面积为
3
3
2
的锐角△ABC的内角，
∴A=
π
3
．（10分）
∵S△ABC=
1
2
AB•ACsinA=
3
2
3
，
∴AC=3．（12分）
由余弦定理得：BC2=AC2+AB2-2•AB•ACcosA=7，
∴BC=
7
．（14分）
练习册系列答案
相关题目
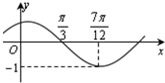精英家教网已知函数f（x）=Msin（ωx+φ）（其中M＞0，ω＞0，|φ|＜
π
2
）的图象如图所示．
（1）求函数f（x）的表达式；
（2）设α∈(
π
6
，  
2π
3
)，  β∈(-
5π
6
，-
π
3
)，  f(
α
2
)=
3
5
，  f(
β
2
)=-
4
5
，求cos2（α-β）的值．
设函数f（x）是奇函数，并且在R上为增函数，若0≤θ≤
π
2
时，f（msinθ）+f（1-m）＞0恒成立，则实数m的取值范围是（　　）
设函数f（x）=x3+x，x∈R．若当0＜θ＜
π
2
时，不等式f（msinθ）+f（1-m）＞0恒成立，则实数m的取值范围是（　　）
（2013•泸州一模）已知命题p：夹角为m的单位向量a，b使|a-b|＞l，命题q：函数f（x）=msin（mx）的导函数为f′（x），若?xo∈R，f′(xo)≥
4π25
．设符合p∧q为真的实数m的取值的集合为A．
（I）求集合A；
（Ⅱ）若B={x∈R|x2=πa}，且B∩A=∅，求实数a的取值范围．
设?＞0，m＞0，若函数f（x）=msin
ωx
2
cos
ωx
2
在区间(-
π
3
，
π
4
)上单调递增，则ω的取值范围是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网