题目内容
一个盒子中有标号分别是1、2、3、4、5的五个大小形状完全相同的小球,现从盒子中随机摸球.
(1)从盒中依次摸两次球,每次摸1个,摸出的球不放回,若两次摸出球上的数字全是奇数或全是偶数为胜,则某人摸球两次取胜的概率是多大?
(2)从盒子中依次摸球,每次摸球1个,摸出的球不放回,当摸出记有奇数的球即停止摸球,否则继续摸球,求摸球次数X的分布列和期望.
(1)从盒中依次摸两次球,每次摸1个,摸出的球不放回,若两次摸出球上的数字全是奇数或全是偶数为胜,则某人摸球两次取胜的概率是多大?
(2)从盒子中依次摸球,每次摸球1个,摸出的球不放回,当摸出记有奇数的球即停止摸球,否则继续摸球,求摸球次数X的分布列和期望.
分析:(1)若某人摸球两次且不放回取胜,根据规定:则两次摸出球上的数字全是奇数或全是偶数.从这5个数中依次取两个数的方法有
种,从1、3、5三个数中依次取两个数有
种,从2、4两个数中依次取两个数有
,进而根据互斥事件的概率计算公式即可得出;
(2)若第一次摸出的球的标号是从1、3、5三个奇数中摸出的可有
种方法,而从给出的5个球中任意摸出一个球可有
种方法,根据概率的计算公式即可求出P(X=1),同理即可计算出P(X=2),P(X=3),即可得出其分布列.再利用相互独立事件的概率、数学期望的公式即可得出.
| A | 2 5 |
| A | 2 3 |
| A | 2 2 |
(2)若第一次摸出的球的标号是从1、3、5三个奇数中摸出的可有
| A | 1 3 |
| A | 1 5 |
解答:解:(1)由题意可得:某人摸球两次取胜的概率P=
+
=
;
(2)∵P(X=1)=
=
,P(X=2)=
=
,P(X=3)=
=
,∴其分布列如下表:
其数学期望EX=1×
+2×
+3×
=
.
| ||
|
| ||
|
| 2 |
| 5 |

(2)∵P(X=1)=
| ||
|
| 3 |
| 5 |
| ||||
|
| 3 |
| 10 |
| ||||||
|
| 1 |
| 10 |
其数学期望EX=1×
| 3 |
| 5 |
| 3 |
| 10 |
| 1 |
| 10 |
| 3 |
| 2 |
点评:弄清题意和熟练掌握排列、组合、互斥和相互独立事件的概率及其数学期望的计算公式是解题的关键.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
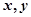 ,设
,设 ,
,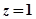 ”发生的概率;
”发生的概率; 的最大值,并求事件“
的最大值,并求事件“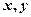 ,设
,设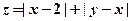 ,
, ”发生的概
”发生的概 率;
率; 的最大值,并求事件“
的最大值,并求事件“