题目内容
 如图,△ABC中,AB=AC=2,BC=2
如图,△ABC中,AB=AC=2,BC=2| 3 |
分析:由A向BC作垂线,垂足为E,根据三角形为等腰三角形求得BE,进而再Rt△ABE中,利用BE和AB的长求得B,则AE可求得,然后在Rt△ADE中利用AE和∠ADC求得AD.
解答:解:由A向BC作垂线,垂足为E,
∵AB=AC
∴BE=
BC=
∵AB=2
∴cosB=
=
∴B=30°
∴AE=BE•tan30°=1
∵∠ADC=45°
∴AD=
=
故答案为:
∵AB=AC
∴BE=
| 1 |
| 2 |
| 3 |
∵AB=2
∴cosB=
| BE |
| AB |
| ||
| 2 |
∴B=30°
∴AE=BE•tan30°=1
∵∠ADC=45°
∴AD=
| AE |
| sin∠ADC |
| 2 |
故答案为:
| 2 |
点评:本题主要考查了解三角形问题.考查了学生分析问题和解决问题的能力.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
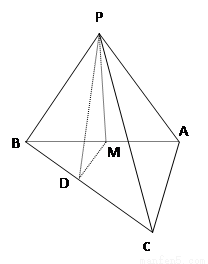
 如图,△ABC中,∠A=90°,AB=4,AC=3,平面ABC外一点P在平面ABC内的射影是AB中点M,二面角P-AC-B的大小为45°.
如图,△ABC中,∠A=90°,AB=4,AC=3,平面ABC外一点P在平面ABC内的射影是AB中点M,二面角P-AC-B的大小为45°. 如图在△ABC中,AB⊥AC,
如图在△ABC中,AB⊥AC,