Question

（2013•宁波模拟）如图，△ABC中，∠B=90°，AB=

2

，BC=1，D、 E两点分别在线段AB、AC上，满足

AD

AB

=

AE

AC

=λ，λ∈(0，1)．现将△ABC沿DE折成直二面角A-DE-B．
（1）求证：当λ=

1

2

时，面ADC⊥面ABE；
（2）当λ∈（0，1）时，直线AD与平面ABE所成角能否等于

π

6

？若能，求出λ的值；若不能，请说明理由．

Answer 1

分析：（1）由题意可得∠ADB为二面角A-DE-B平面角，且∠ADB=

π

2

，可得AD⊥BE，由λ=

1

2

结合三角形的相似可得BE⊥DC，由线面垂直的判断定理可得；
（2）连结BE，过点D作DH⊥BE于H，连结AH，过点D作DO⊥AH于O．可证∠DAO为AD与平面ABE所成角，由三角形的知识可建立关于λ的方程，解之可得．

解答：解：（1）∵

AD

AB

=

AE

AC

=λ，∴DE∥BC，∴DE⊥AD，DE⊥BD，
∴∠ADB为二面角A-DE-B平面角，且∠ADB=

π

2

．           （2分）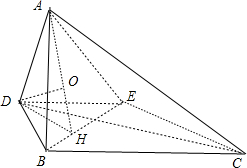
∴AD⊥面BCD，又∵BE?面BCD，∴AD⊥BE（4分）
又当λ=

1

2

时，BD=

2

2

，DE=

1

2

，BC=1，可得

BD

DE

=

BC

BD

，
∴△BDE∽△DBC，∴∠EBD=∠DCB，∴BE⊥DC    （6分）
∴BE⊥面ADC，又BE?面ABE，∴面ABE⊥面ADC    （7分）
（2）连结BE，过点D作DH⊥BE于H，连结AH，过点D作DO⊥AH于O．如图：
∵AD⊥BE，BE⊥DH∴BE⊥面ADHDO?面ADH，∴BE⊥DO，又DO⊥AH，
∴DO⊥面ABE，所以∠DAO为AD与平面ABE所成角         （10分）
在Rt△ADH中，tan∠DAO=

DH

DA

，Rt△BDE中，BD=

2

(1-λ)，DE=λ，
∴DH=

2 (1-λ)λ

λ2+2(1-λ)2

，又AD=

2

λ，
若∠DAO=

π

6

，则

(1-λ)

λ2+2(1-λ)2

=

3

3

，解得λ=

1

2

（14分）

点评：本题考查直线与平面垂直的判定，涉及线面角和二面角，属中档题．