题目内容
已知直线a2x＋y＋2＝0与直线bx－(a2＋1)y－1＝0互相垂直，则|ab|的最小值为 ( )
| A．5 | B．4 | C．2 | D．1 |
C
解析试题分析：由已知有
，∴
，∴
.
考点：1.两直线垂直的充要条件；2.均值定理的应用.
练习册系列答案
相关题目
若正数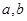
满足：
，则
的最小值为（ ）
A． | B． | C． | D． |
下列各式中，最小值等于２的是（ ）
A． | B． |
C． | D． |
若直线
被圆
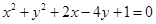截得的弦长为4，则
的最小值是（ ）
| A．16 | B．9 | C．12 | D．8 |
若直线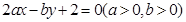
被圆
截得的弦长为4，则
的最小值是( )
| A．16 | B．9 | C．12 | D．8 |
若
,则
的取值范围是（ ）
A． | B． | C． | D． |
当x>1时，不等式x－2＋
≥
恒成立，则实数的取值范围是 ( )
| A．(－∞，0] | B．[0，＋∞) | C．[1，＋∞) | D．(－∞，1] |
设
、
为正数，则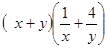
的最小值为（ ）
A． | B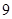． | C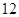． | D． |
若2x+2y=1,则x+y的取值范围是( )
| A．[0,2] | B．[-2,0] |
| C．[-2,+∞) | D．(-∞,-2] |