题目内容
若直线 被圆
被圆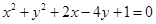 截得的弦长为4,则
截得的弦长为4,则 的最小值是( )
的最小值是( )
| A.16 | B.9 | C.12 | D.8 |
B
解析试题分析:由圆的方程可知圆心坐标为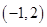 ,半径为2,又直线被圆截得的弦长为4,所以直线过圆心,将圆心坐标代入直线方程得
,半径为2,又直线被圆截得的弦长为4,所以直线过圆心,将圆心坐标代入直线方程得 ,则
,则 ,当且仅当
,当且仅当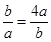 ,即
,即 时等号成立.故正确答案为B.
时等号成立.故正确答案为B.
考点:1.直线与圆的位置关系;2.基本不等式.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
设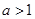 ,
,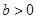 ,若
,若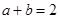 ,则
,则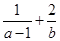 的最小值为( )
的最小值为( )
A.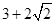 | B.6 | C.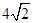 | D.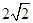 |
已知关于x的不等式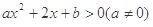 的解集是
的解集是 ,且a>b,则
,且a>b,则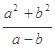 的最小值是( )
的最小值是( )
A.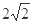 | B.2 | C.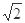 | D.1 |
若 和
和 均为非零实数,则下列不等式中恒成立的是( )
均为非零实数,则下列不等式中恒成立的是( )
A. . . | B.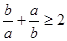 . . |
C.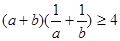 . . | D.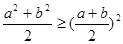 . . |
若正数 满足
满足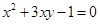 ,则
,则 的最小值是( )
的最小值是( )
A. | B. | C.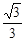 | D. |
若实数 、
、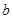 、
、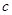 、
、 满足
满足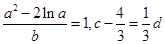 ,则
,则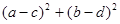 的最小值 为 ( )
的最小值 为 ( )
A.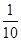 | B.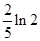 | C.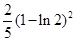 | D.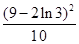 |
若a,b∈R,且ab>0,则下列不等式中,恒成立的是( )
A.a+b≥2  | B.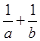 > > | C.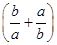 ≥2 ≥2 | D.a2+b2>2ab |
已知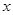 ,
, ,且
,且 ,则
,则 的最大值是( )
的最大值是( )
| A.3 | B.3.5 | C.4 | D.4.5 |