题目内容
2.已知数列{bn}是首项为b1=1,公差d=3的等差数列,bn=l-3log2 (2an)(n∈N*).(1)求证:{an}是等比数列;
(2)若数列{cn}满足cn=an•bn,求数列{cn}的前n项和Sn.
分析 (1)由题意得3n-2=1-3log2(2an),从而${a}_{n}=(\frac{1}{2})^{n}$,由此能证明数列{an}是等比数列.
(2)由=$(3n-2)•(\frac{1}{2})^{n}$,n∈N*,由此利用错位相减法能求出数列{cn}的前n项和Sn.
解答 解:(1)∵数列{bn}是首项为b1=1,公差d=3的等差数列,
∴由题意bn=1+3(n-1)=3n-2,…(2分)
则由bn=l-3log2 (2an)(n∈N*),得3n-2=1-3log2(2an),则${a}_{n}=(\frac{1}{2})^{n}$,
∴$\frac{{a}_{n}}{{a}_{n-1}}=\frac{(\frac{1}{2})^{n}}{(\frac{1}{2})^{n-1}}$=$\frac{1}{2}$,(n≥2,n∈N*),…(4分)
故数列{an}是首项为$\frac{1}{2}$,公比为$\frac{1}{2}$的等比数列.…(5分)
(2)由(1)知,cn=$(3n-2)•(\frac{1}{2})^{n}$,n∈N*,…(6分)
∴${S}_{n}=1×\frac{1}{2}+4×(\frac{1}{2})^{2}+7×(\frac{1}{2})^{3}$+…+(3n-5)×($\frac{1}{2}$)n-1+(3n-2)×($\frac{1}{2}$)n,
∴$\frac{1}{2}{S}_{n}$=1×($\frac{1}{2}$)2+4×($\frac{1}{2}$)3+7$\frac{1}{2}$)4+…+(3n-5)×($\frac{1}{2}$)n+(3n-2)×($\frac{1}{2}$)n+1,…(8分)
两式相减得 $\frac{1}{2}{S}_{n}$=$\frac{1}{2}+3[(\frac{1}{2})^{2}+(\frac{1}{2})^{3}+(\frac{1}{2})^{4}+…+(\frac{1}{2})^{n}]$-(3n-2)×($\frac{1}{2}$)×($\frac{1}{2}$)n+1,
化简,得$\frac{1}{2}{S}_{n}=2-(3n+4)×(\frac{1}{2})^{n+1}$,…(11分)
所以${S}_{n}=4-(3n+4)×(\frac{1}{2})^{n}$,n∈N*.…(12分)
点评 本题考查等比数列的证明,考查数列的前n项和的求法,是中档题,解题时要认真审题,注意错位相减法的合理运用.

 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案| A. | $\sqrt{2}$ | B. | $\frac{9}{8}$ | C. | 1 | D. | $\frac{7}{8}$ |
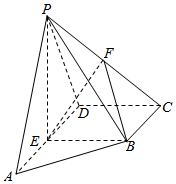 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,四边形ABCD为直角梯形,BC∥AD,∠ADC=90°,BC=CD=$\frac{1}{2}$AD=1,PA=PD,E,F分别为线段AD,PC的中点.
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,四边形ABCD为直角梯形,BC∥AD,∠ADC=90°,BC=CD=$\frac{1}{2}$AD=1,PA=PD,E,F分别为线段AD,PC的中点.