题目内容
已知函数 ,数列{an}满足an=f(an-1)(n≥2,n∈N+).
,数列{an}满足an=f(an-1)(n≥2,n∈N+).
(Ⅰ)若 ,数列{bn}满足
,数列{bn}满足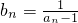 ,求证:数列{bn}是等差数列;
,求证:数列{bn}是等差数列;
(Ⅱ)若 ,数列{an}中是否存在最大项与最小项,若存在,求出最大项与最小项;若不存在,说明理由;
,数列{an}中是否存在最大项与最小项,若存在,求出最大项与最小项;若不存在,说明理由;
(Ⅲ)若1<a1<2,试证明:1<an+1<an<2.
解:∵ ,则
,则 (n≥2,n?N*).
(n≥2,n?N*).
(Ⅰ) ,
, ,
,
∴ .
.
∴数列{bn}是等差数列.
(Ⅱ)由(Ⅰ)知,数列{bn}是等差数列,首项 ,公差为1,
,公差为1,
则其通项公式 ,
,
由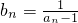 得
得 ,
,
故 .
.
考查函数 ,
,
则 .
.
则函数 在区间
在区间 ,
, 上为减函数.
上为减函数.
∴当 时,
时, ,
,
且在 上递减,故当n=3时,an取最小值
上递减,故当n=3时,an取最小值
∴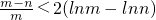 ;
;
当 时,
时, ,
,
且在 上递减,故当n=4时,an取最大值
上递减,故当n=4时,an取最大值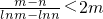 .故存在.
.故存在.
(Ⅲ)先用数学归纳法证明1<an<2,再证明an+1<an.
①当n=1时,1<a1<2成立,
②假设n=k时命题成立,即1<ak<2,
则当n=k+1时, ,
, ,则1<ak+1<2,故当n=k+1时也成立.
,则1<ak+1<2,故当n=k+1时也成立.
综合①②有,命题对任意n?N*时成立,即1<an<2.下证an+1<an.
∵ ,
,
∴an+1<an.
综上所述:1<an+1<an<2.
分析:(Ⅰ)根据题设中的函数式,求得an和an-1的递推式,进而利用bn-bn-1=1判断出数列{bn}是等差数列.
(Ⅱ)根据(Ⅰ)可求得,数列{bn}的通项公式,则bn可得,通过对函数 求导判断出则函数
求导判断出则函数 在区间
在区间 ,
, 上为减函数.且在
上为减函数.且在 上递减,故当n=3时,an取最小值进而可知当
上递减,故当n=3时,an取最小值进而可知当 时,
时, ,且在
,且在 上递减,故当n=4时,an取最大值
上递减,故当n=4时,an取最大值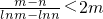 .
.
(Ⅲ)先看当n=1时等式成立,再看n≥2时,假设n=k时命题成立,即1<ak<2,则当n=k+1时, ,则1<ak+1<2,
,则1<ak+1<2, 故当n=k+1时也成立.进而an+1-an<0判断出an+1<an.
故当n=k+1时也成立.进而an+1-an<0判断出an+1<an.
最后综合可证明原式.
点评:本题主要考查了数列与不等式的综合,数学归纳法的证明方法.考查了学生综合分析问题的能力和基本的推理能力.
 ,则
,则 (n≥2,n?N*).
(n≥2,n?N*).(Ⅰ)
 ,
, ,
,∴
 .
.∴数列{bn}是等差数列.
(Ⅱ)由(Ⅰ)知,数列{bn}是等差数列,首项
 ,公差为1,
,公差为1,则其通项公式
 ,
,由
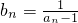 得
得 ,
,故
 .
.考查函数
 ,
,则
 .
.则函数
 在区间
在区间 ,
, 上为减函数.
上为减函数.∴当
 时,
时, ,
,且在
 上递减,故当n=3时,an取最小值
上递减,故当n=3时,an取最小值∴
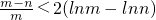 ;
;当
 时,
时, ,
,且在
 上递减,故当n=4时,an取最大值
上递减,故当n=4时,an取最大值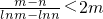 .故存在.
.故存在.(Ⅲ)先用数学归纳法证明1<an<2,再证明an+1<an.
①当n=1时,1<a1<2成立,
②假设n=k时命题成立,即1<ak<2,
则当n=k+1时,
 ,
, ,则1<ak+1<2,故当n=k+1时也成立.
,则1<ak+1<2,故当n=k+1时也成立.综合①②有,命题对任意n?N*时成立,即1<an<2.下证an+1<an.
∵
 ,
,∴an+1<an.
综上所述:1<an+1<an<2.
分析:(Ⅰ)根据题设中的函数式,求得an和an-1的递推式,进而利用bn-bn-1=1判断出数列{bn}是等差数列.
(Ⅱ)根据(Ⅰ)可求得,数列{bn}的通项公式,则bn可得,通过对函数
 求导判断出则函数
求导判断出则函数 在区间
在区间 ,
, 上为减函数.且在
上为减函数.且在 上递减,故当n=3时,an取最小值进而可知当
上递减,故当n=3时,an取最小值进而可知当 时,
时, ,且在
,且在 上递减,故当n=4时,an取最大值
上递减,故当n=4时,an取最大值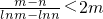 .
.(Ⅲ)先看当n=1时等式成立,再看n≥2时,假设n=k时命题成立,即1<ak<2,则当n=k+1时,
 ,则1<ak+1<2,
,则1<ak+1<2, 故当n=k+1时也成立.进而an+1-an<0判断出an+1<an.
故当n=k+1时也成立.进而an+1-an<0判断出an+1<an.最后综合可证明原式.
点评:本题主要考查了数列与不等式的综合,数学归纳法的证明方法.考查了学生综合分析问题的能力和基本的推理能力.

练习册系列答案
相关题目
 ,数列an满足
,数列an满足 .
.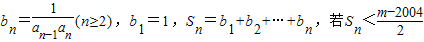 对一切n∈N*成立,求最小正整数m.
对一切n∈N*成立,求最小正整数m.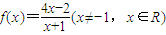 ,数列{an}满足 a1=a(a≠-1,a∈R),an+1=f(an)(n∈N*).
,数列{an}满足 a1=a(a≠-1,a∈R),an+1=f(an)(n∈N*). ,证明数列{bn}是等比数列,并求出通项公式an.
,证明数列{bn}是等比数列,并求出通项公式an. 若数列{an}满足an=
若数列{an}满足an= (n∈N+)且{an}是递减数列,则实数a的取值范围是( )
(n∈N+)且{an}是递减数列,则实数a的取值范围是( ) ,1) B.(
,1) B.(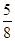 ) C.(
) C.( ) D.(
) D.( ,数列an满足an=f(n)(n∈N*),且an是递增数列,则实数a的取值范围是
,数列an满足an=f(n)(n∈N*),且an是递增数列,则实数a的取值范围是