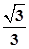题目内容
(本小题满分13分)
在平面直角坐标系中,已知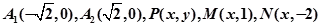 ,若实数
,若实数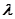 使得
使得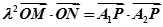 (
(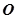 为坐标原点)
为坐标原点)
(1)求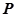 点的轨迹方程,并讨论
点的轨迹方程,并讨论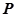 点的轨迹类型;
点的轨迹类型;
(2)当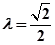 时,若过点
时,若过点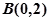 的直线与(1)中
的直线与(1)中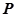 点的轨迹交于不同的两点
点的轨迹交于不同的两点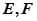 (
(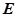 在
在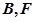 之间),试求
之间),试求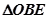 与
与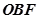 面积之比的取值范围。
面积之比的取值范围。
在平面直角坐标系中,已知
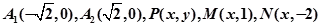 ,若实数
,若实数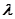 使得
使得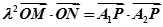 (
(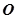 为坐标原点)
为坐标原点)(1)求
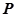 点的轨迹方程,并讨论
点的轨迹方程,并讨论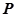 点的轨迹类型;
点的轨迹类型;(2)当
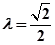 时,若过点
时,若过点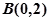 的直线与(1)中
的直线与(1)中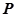 点的轨迹交于不同的两点
点的轨迹交于不同的两点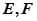 (
(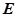 在
在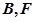 之间),试求
之间),试求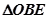 与
与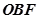 面积之比的取值范围。
面积之比的取值范围。(1)
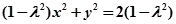 ;
;1.
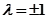 时方程为
时方程为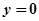 轨迹为一条直线;
轨迹为一条直线; ③.
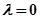 时方程为
时方程为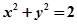 轨迹为圆;
轨迹为圆;③.
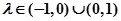 时方程为
时方程为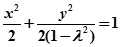 轨迹为椭圆 ;
轨迹为椭圆 ;④.
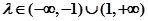 时方程为
时方程为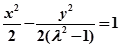 轨迹为双曲线;
轨迹为双曲线;(2)
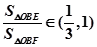
第一问利用向量的坐标公式得到。
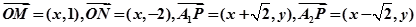
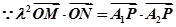
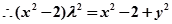 化简得:
化简得: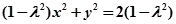
第二问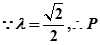 点轨迹方程为
点轨迹方程为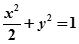 ,
,

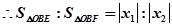
设直线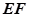 直线方程为
直线方程为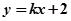 ,联立方程可得:
,联立方程可得: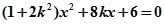 。
。
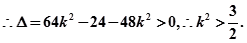
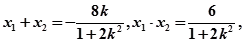
结合韦达定理的得到。
解:(1)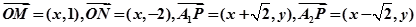
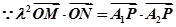
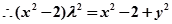 化简得:
化简得: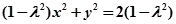 ......2
......2
1.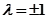 时方程为
时方程为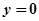 轨迹为一条直线......3
轨迹为一条直线......3
③.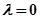 时方程为
时方程为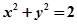 轨迹为圆......4
轨迹为圆......4
③.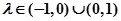 时方程为
时方程为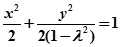 轨迹为椭圆 .......5
轨迹为椭圆 .......5
④.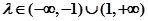 时方程为
时方程为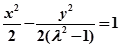 轨迹为双曲线。 ....6
轨迹为双曲线。 ....6
(2)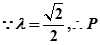 点轨迹方程为
点轨迹方程为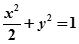 ,
,
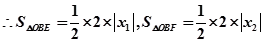
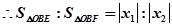 ......7
......7
设直线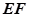 直线方程为
直线方程为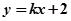 ,联立方程可得:
,联立方程可得: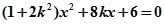 。
。
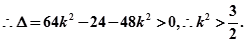
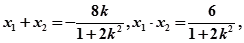
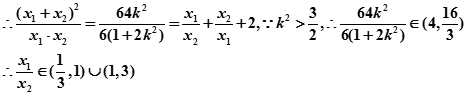 .10
.10
由题意可知: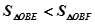 ,所以
,所以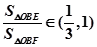 .....12
.....12
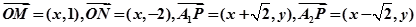
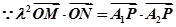
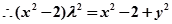 化简得:
化简得: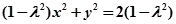
第二问
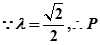 点轨迹方程为
点轨迹方程为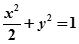 ,
,
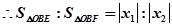
设直线
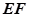 直线方程为
直线方程为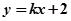 ,联立方程可得:
,联立方程可得: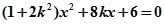 。
。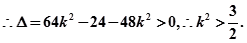
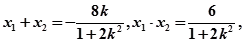
结合韦达定理的得到。
解:(1)
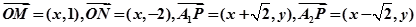
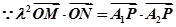
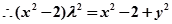 化简得:
化简得: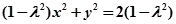 ......2
......21.
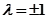 时方程为
时方程为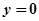 轨迹为一条直线......3
轨迹为一条直线......3 ③.
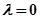 时方程为
时方程为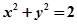 轨迹为圆......4
轨迹为圆......4③.
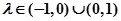 时方程为
时方程为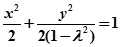 轨迹为椭圆 .......5
轨迹为椭圆 .......5④.
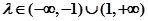 时方程为
时方程为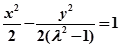 轨迹为双曲线。 ....6
轨迹为双曲线。 ....6(2)
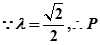 点轨迹方程为
点轨迹方程为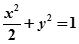 ,
,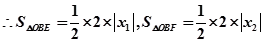
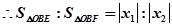 ......7
......7设直线
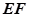 直线方程为
直线方程为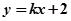 ,联立方程可得:
,联立方程可得: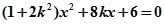 。
。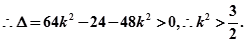
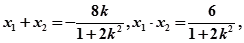
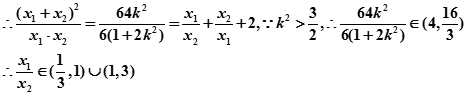 .10
.10由题意可知:
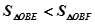 ,所以
,所以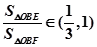 .....12
.....12
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
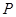 是曲线
是曲线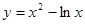 上任意一点, 则点
上任意一点, 则点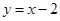 的距离的最小值
的距离的最小值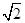
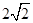
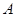 、
、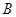 分别是直线
分别是直线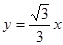 和
和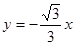 上的两个动点,线段
上的两个动点,线段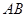 的长为
的长为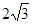 ,
,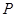 是
是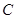 的方程;
的方程;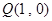 任意作直线
任意作直线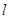 (与
(与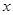 轴不垂直),设
轴不垂直),设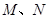 两点,与
两点,与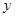 轴交于
轴交于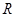 点.若
点.若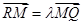 ,
,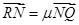 ,证明:
,证明: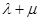 为定值.
为定值.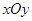 中,设点
中,设点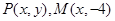 ,坐标原点
,坐标原点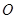 在以线段
在以线段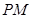 为直径的圆上
为直径的圆上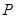 的轨迹C的方程;
的轨迹C的方程;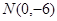 的直线
的直线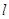 与轨迹C交于两点
与轨迹C交于两点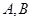 ,点
,点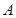 关于
关于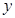 轴的对称点为
轴的对称点为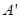 ,试判断直线
,试判断直线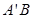 是否恒过一定点,并证明你的结论.
是否恒过一定点,并证明你的结论.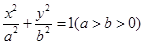 的左、右顶点分别为
的左、右顶点分别为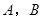 ,点
,点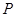 在椭圆上且异于
在椭圆上且异于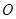 为坐标原点.
为坐标原点.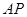 与
与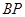 的斜率之积为
的斜率之积为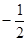 ,求椭圆的离心率;
,求椭圆的离心率;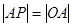 ,证明直线
,证明直线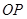 的斜率
的斜率 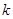 满足
满足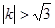
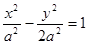 (a>0),抛物线C2的顶点在原点O,C2的焦点是C1的左焦点F1。
(a>0),抛物线C2的顶点在原点O,C2的焦点是C1的左焦点F1。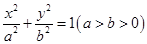 的左、右焦点分别为
的左、右焦点分别为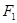 ,
,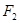 , 点
, 点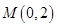 是椭圆的一个顶点,△
是椭圆的一个顶点,△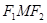 是等腰直角三角形.
是等腰直角三角形.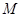 分别作直线
分别作直线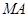 ,
,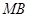 交椭圆于
交椭圆于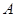 ,
,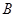 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为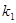 ,
,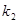 ,且
,且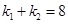 ,证明:直线
,证明:直线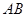 过定点(
过定点(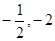 ).
).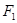 、
、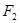 是椭圆
是椭圆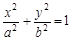
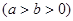 的左、右焦点,
的左、右焦点,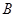 是该椭圆短轴的一个端点,直线
是该椭圆短轴的一个端点,直线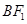 与椭圆
与椭圆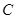 交于点
交于点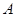 ,若
,若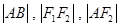 成等差数列,则该椭圆的离心率为 .
成等差数列,则该椭圆的离心率为 .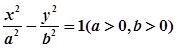 的离心率为2,则
的离心率为2,则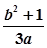 的最小值为( )
的最小值为( )