题目内容
如图平面四边形ABCD中,AB=AD=a,BC=CD=BD 设∠BAD=θ(I)将四边形ABCD的面积S表示为θ的函数.
(II)求四边形ABCD面积S的最大值及此时θ值.

【答案】分析:(I)在△BAD中,由余弦定理求BD,从而可求四边形ABCD的面积;
(II)将四边形的面积化简,确定角的范围,利用三角函数的图象,即可求得四边形ABCD面积S的最大值.
解答:解:(I)在△BAD中,由余弦定理可得 =
=
∴四边形ABCD的面积S= +
+ ×[2a2(1-cosθ)]=
×[2a2(1-cosθ)]= +a2(
+a2( )
)
= +a2sin(
+a2sin( )(0<θ<π)
)(0<θ<π)
(II)∵0<θ<π,∴
∴ <sin(
<sin( )≤1
)≤1
当且仅当 ,即
,即 时,sin(
时,sin( )取得最大值1
)取得最大值1
四边形ABCD面积S的最大值为 +a2,此时
+a2,此时 .
.
点评:本题考查三角函数知识,考查余弦定理的运用,考查三角函数的性质,属于中档题.
(II)将四边形的面积化简,确定角的范围,利用三角函数的图象,即可求得四边形ABCD面积S的最大值.
解答:解:(I)在△BAD中,由余弦定理可得
 =
=
∴四边形ABCD的面积S=
 +
+ ×[2a2(1-cosθ)]=
×[2a2(1-cosθ)]= +a2(
+a2( )
)=
 +a2sin(
+a2sin( )(0<θ<π)
)(0<θ<π)(II)∵0<θ<π,∴

∴
 <sin(
<sin( )≤1
)≤1当且仅当
 ,即
,即 时,sin(
时,sin( )取得最大值1
)取得最大值1四边形ABCD面积S的最大值为
 +a2,此时
+a2,此时 .
.点评:本题考查三角函数知识,考查余弦定理的运用,考查三角函数的性质,属于中档题.

练习册系列答案
相关题目

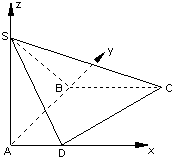 如图,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
如图,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD= 如图,四边形ABCD中,△ABC为正三角形,AD=AB=2,BD=2
如图,四边形ABCD中,△ABC为正三角形,AD=AB=2,BD=2 (2012•包头一模)如图,四边形DCBE为直角梯形,∠DCB=90°,DE∥CB,DE=1,BC=2,又AC=1,∠ACB=120°,CD⊥AB,直线AE与直线CD所成角为60°.
(2012•包头一模)如图,四边形DCBE为直角梯形,∠DCB=90°,DE∥CB,DE=1,BC=2,又AC=1,∠ACB=120°,CD⊥AB,直线AE与直线CD所成角为60°.