题目内容
已知某工厂生产 件产品的成本为
件产品的成本为 (元),
(元),
问:(1)要使平均成本最低,应生产多少件产品?
(2)若产品以每件500元售出,要使利润最大,应生产多少件产品?
(1) 1000 ;(2) 6000.
解析试题分析:(1)先根据题意设生产x件产品的平均成本为y元,再结合平均成本的含义得出函数y的表达式,最后利用导数求出此函数的最小值即可;
(2)先写出利润函数的解析式,再利用导数求出此函数的极值,从而得出函数的最大值,即可解决问题:要使利润最大,应生产多少件产品..
试题解析:解:(1)设平均成本为 元,则
元,则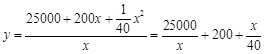 ,
,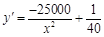 ,令
,令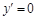 得
得 .
.
当在 附近左侧时
附近左侧时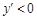 ;
;
在 附近右侧时
附近右侧时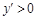 ,故当
,故当 时,
时, 取极小值,而函数只有一个点使
取极小值,而函数只有一个点使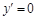 ,故函数在该点处取得最小值,因此,要使平均成本最低,应生产1000件产品. 6分;
,故函数在该点处取得最小值,因此,要使平均成本最低,应生产1000件产品. 6分;
(2)利润函数为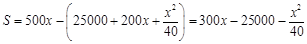 ,
,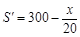 ,
,
令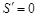 ,得
,得 ,当在
,当在 附近左侧时
附近左侧时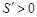 ;在
;在 附近右侧时
附近右侧时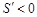 ,故当
,故当 时,
时,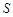 取极大值,而函数只有一个点使
取极大值,而函数只有一个点使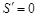 ,故函数在该点处取得最大值,因此,要使利润最大,应生产6000件产品. 12分;
,故函数在该点处取得最大值,因此,要使利润最大,应生产6000件产品. 12分;
考点:导数的应用.

练习册系列答案
相关题目
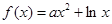 (
(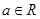 )
)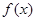 在区间[e,e2]上的最大值和最小值;
在区间[e,e2]上的最大值和最小值;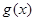 、
、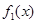 、
、 在公共定义域D上,满足
在公共定义域D上,满足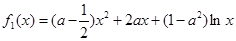 ,
,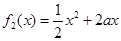 ,若在区间(1,+∞)上,函数
,若在区间(1,+∞)上,函数 ,
,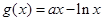 ,其中
,其中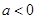 ,
,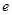 为自然对数的底数.
为自然对数的底数.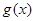 在
在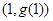 处的切线
处的切线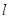 与直线
与直线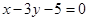 垂直,求
垂直,求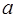 的值;
的值;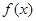 在
在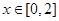 上的最小值;
上的最小值;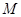 ,使得
,使得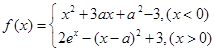 ,
,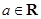 .
.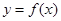 在
在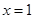 处取得极值,求
处取得极值,求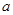 的值;
的值;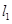 平行于直线
平行于直线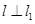 , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程. 的定义域是
的定义域是 ,其中常数
,其中常数 .(注:
.(注: 
 ,求
,求 的过原点的切线方程.
的过原点的切线方程. ,恒有
,恒有 .
. 时,求最大实数
时,求最大实数 ,使不等式
,使不等式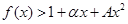 对
对 恒成立.
恒成立. .当
.当 时,函数
时,函数 取得极值
取得极值 .
. 有3个解,求实数
有3个解,求实数 的取值范围.
的取值范围.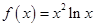 .
. 的单调区间;
的单调区间;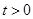 ,存在唯一的
,存在唯一的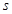 ,使
,使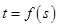 ;
;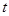 的函数为
的函数为 ,证明:当
,证明:当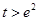 时,有
时,有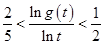 .
.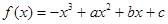 在
在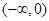 上是减函数,在
上是减函数,在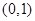 上是增函数,函数
上是增函数,函数 在
在 上有三个零点,且
上有三个零点,且 是其中一个零点.
是其中一个零点.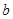 的值;
的值;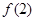 的取值范围;
的取值范围;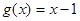 ,且
,且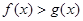 的解集为
的解集为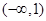 ,求实数
,求实数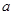 的取值范围.
的取值范围.